Significant Digits and Engineering Units

Learn the basics of using significant digits for mitigating error propagation.

When looking at a number, there are rules to determine which digits are significant and which aren't. As a byproduct of these rules, when the time arises to take measurements and perform several math operations to arrive at a resolution, it's important to consider these rules and to round appropriately in order to mitigate error propagation. Below is a list of rules one should follow in order to determine if a given digit is considered significant.

The following ARE significant digits:

● Zeros that are within a number (EX: 240503)

● Zeros that aren't used to hold a decimal point (EX:  98.600)

● All non-zero numbers (EX: 123456789)

The following are NOT significant digits:

● Zeros that set the decimal point (EX: 0.0025)

The following might be significant, depending on the situation:

● Zeros that follow a number (EX: 1200)

The last bullet can be applicable for both categories as it is a condition that is subjective for each case. It is common to round to an even 100, such as the example 1200, but the figure may be accurate to 4 places making 1200 contain 4 significant digits. Some people even underline the last significant figure in a number in order to mitigate ambiguity.

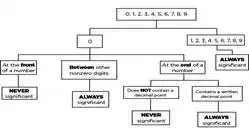
A flow chart for visual learners.

Reducing Error Propagation

When applying mathematics to significant figures, the answer will usually carry forward the least number of significant digits as any term from the problem. If I have 3 terms and 2 of them have 4 significant figures and the third has 2 significant figures, then the answer will normally only have 2 significant digits. The mathematical resolution is only as sound as the most uncertain term (AKA a chain is only as strong as its weakest link). There are some instances where simplification will not work, here are a few examples:

● 12345 + 23 = 12358 (it does NOT become 12000 just because one of the operands only has two significant figures).

● 823 + 491 = 1314 (the answer has more significant figures than either of the operands).

When terms can't be simplified, you must determine their uncertainty, which is a range of numbers that the true value lies between. It's good practice when taking measurements to always maximize the resolution of a given measurement, knowing that after calculations are complete there will be rounding that will reduce the precision of the measurements in question.

Engineering Units

Engineering notation is a version of scientific notation that is written in powers of 10, where the exponents are multiples of 3. Every 3rd power of 10 has a prefix associated with it, for both greater and less than zero. The most common units are below:

● Tera  1012

● Giga  109

● Mega 106

● Kilo    103

● Milli    10-3

● Micro  10-6

● Nano  10-9

● Pico   10-12

The following statements are equivalent and each has the same number of significant digits:

This input can handle 20A.

This input can handle 20000mA.

This input can handle 0.02kA.

Conclusion

The rules governing significant digits are designed to carry forward meaningful data, such that the mathematical resolution contains the least amount of uncertainty. Adhering to the rules is not only good practice but also the best method to mitigate error propagation. 

BONUS: Since it's not a native format if you would like to use engineering notation in Excel, use the following custom format for the cells you wish to display:

###.###E+0