Annual Worth Calculations
The AW method is commonly used for comparing alternatives. As illustrated in Chapter 4, AW means that all incomes and disbursements (irregular and uniform) are converted into an equivalent uniform annual (end-of-period) amount, which is the same each period. The major advantage of this method over all the other methods is that it does not require making the comparison over the least common multiple (LCM) of years when the alternatives have different lives. That is, the AW value of the alternative is calculated for one life cycle only. If the project is continued for more than one cycle, the equivalent annual worth for the next cycle and all succeeding cycles will be exactly the same as for the first, provided all cash flows are the same for each cycle in constant-value dollars (discussed in Chapter 12).
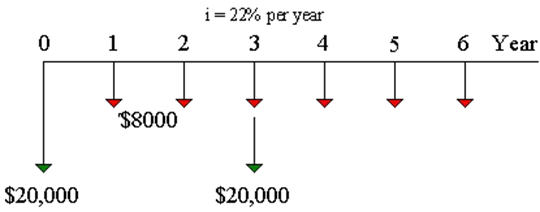
The repeatability of the uniform annual series through various life cycles can be demonstrated by considering the cash-flow diagram in Figure 6-1, which represents two life cycles of an asset with a first cost of $20,000, an annual operating cost of $8000, and a 3-year life.
The AW for one life cycle (i.e., 3 years) would be calculated as follows:
AW = -20,000 (A/P, 22%, 3) – 8000
= -$17,793
The AW for two life cycles is calculated as
AW = -20,000 (A/P, 22%, 6) – (20,000)(P/F, 22%, 3)(A/P, 22%, 6) – 8000
= -$17,793
The AW value for the first life cycle is exactly the same as that for two life cycles. This same AW will be obtained when three, four, or any other number of life cycles are evaluated. Thus, the AW for one life cycle of an alternative represents the equivalent uniform annual worth of that alternative every time the cycle is repeated.

When an asset has a terminal salvage value, there are several ways by which the AW can be calculated. The two that will be discussed here are the salvage sinking fund method, which is represented by the general equation:
AW = -P (A/P, i, n) + S (A/F, i, n)
And the capital recovery plus interest method, which is represented by
AW = -(P – S) (A/P, i, n) – Si
Their equivalence can be demonstrated by considering an asset which has a first cost of $20,000, an annual operating cost of $10,000 per year, and a $5000 salvage value at the end of its 5 year life. The annual worth at 12% per year by the first method is:
AW = -20,000 (A/P, 12%, 5) – 10,000 + 5000 (A/F,12%, 5)
= -20,000 (0.27741) – 10,000 + 5,000 (0.15741)
= -$14,761
The annual worth by the second method is:
AW = -(20,000 - 5000) (A/P, 12%, 5) - 10,000 - 5000 (0.12)
= -15,000 (0.27741) - 10,000 - 600
= -$14,761
Thus, the AW values are the same by either method, but only the former will be used hereafter.