Interest and Equivalence
Simple interest, as opposed to compound interest, is rare. With an investment that pays simple interest, the amount of interest accumulated each period depends solely on the amount invested, not on prior interest earned and left in the account.
The following single payment equation applies to simple interest: F = P (1 + I * n)
Example: If $100 is invested at 6% interest (compound interest) for four years, the amount accumulated at the end of four years is:

Computing Cash Flows
One way we model financial processes is with cash flow diagrams.
These are horizontal lines that represent time. At various points we place arrows pointing up or down to represent cash going out (payments) or coming in (revenues). Usually, payments are represented as negative, down-pointing, and revenues as positive, up-pointing. However, you will see other representations; within a single financial process you must be consistent. (Remember that EOY means End-Of-Year.)
Consider several cash flows; do not be concerned with why they are occurring:

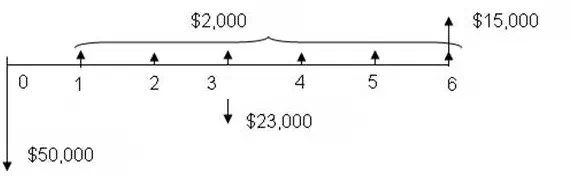
We can see that in some years the cash flow is simple: At EOY 1 the cash flow is positive — that is, revenue — and equals $2,000. In other years, there may be more than one contributor to the cash flow: At EPY 3, the cash flow is composed of the $2,000 annual amount minus the $23,000 one-time expense. Thus, the total cash flow at EOY 3 is $21,000 negative.
What is the cash flow at EOY 6?
Scroll down to check your answer.
Did you get $17,000? Note that at EOY 6, there is the annual received amount of $2000 plus the one-time receipt of $15,000.