CHANGES IN SCALE AND FACTOR PROPORTIONS
Factor proportions are altered by keeping the quantity of one or some factors fixed and varying the quantity of the other. The changes in output as a result of the variation in factor proportions, as seen before, forms the subject-matter of the “law of variable proportions.” We shall now undertake the study of changes in output when all factors or inputs in a particular production function are increased together. In other words, we shall now study the behaviour of output in response to the changes in the scale. An increase in the scale means that all inputs or factors are increased in the same proportion. Increase in the scale thus occurs when all factors or inputs are increased keeping factor proportions unaltered. The study of changes in output as a consequence of changes in the scale forms the subject-matter of ‘returns to scale’.
Before explaining returns to scale it will be instructive to make clear distinction between changes in the scale and changes in factor proportions. The difference between the changes in scale and changes in factor proportions will become clear from the study of Fig. 6 where two factors, labour and capital, have been measured on X-axis and 7-axis respectively. We suppose that only labour and capital are required to produce a particular product. An equal product map has been drawn. A point S has been taken on the Y-axis and the horizontal line ST parallel to X-axis has been drawn. OS represents the amount of capital which remains fixed along the line ST. As we move towards right on the line ST, the amount of labour varies while the amount of capital remains fixed at OS. In other words, proportion between the two factors undergoes a change along the line ST; the ratio of the variable factor ’labour’ to the fixed factor ’capital’ rises as we move to the right on the line ST. Thus the movement along the line ST represents variation in factor proportions. Likewise, a vertical line GH parallel to the Y-axis is drawn which will also indicate changes in factor proportions. But in this case the quantity of labour will remain fixed while the quantity of capital will vary
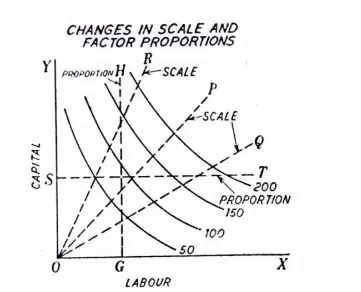
Now, draw a straight line OP passing through the origin. It -will be seen that along the line OP the inputs of both the factors, labour and capital, vary. Moreover, because the line OP is a straight line through the origin, the ratio between the two factors along OP will remain the same throughout. Thus, the upward movement along the line OP indicates the increase in the absolute amounts of two factors employed with the proportion between two factors remaining unchanged. Assuming that only labour and capital are needed to produce a product, then the increase in the two factors along the line OP represents the increase in the scale since along the line OP both the factors increase in the same proportion and therefore proportion between the two factors remains unaltered. If any other straight line through the origin such as OQ or OR is drawn, it will show, like the line OP, the changes in the scale but it will represent a different given proportion of factors which remains the same along the line. That is, the various straight lines through the origin will indicate different proportions between the two factors but on each line the proportion between the two factors will remain the same throughout.