Assortative matching in cities
In most countries around the world, there are large internal wage disparities between cities (Moretti 2011, Combes et al. 2008). Germany is no exception. In 2014, the average hourly wage of a worker in Munich was roughly 43% higher than the wage of a comparable worker (with the same education, age, gender, etc.) in Uelzen, a small city at the bottom of the wage distribution.
Figure 1 Spatial wage disparities in Germany, 1985-2014
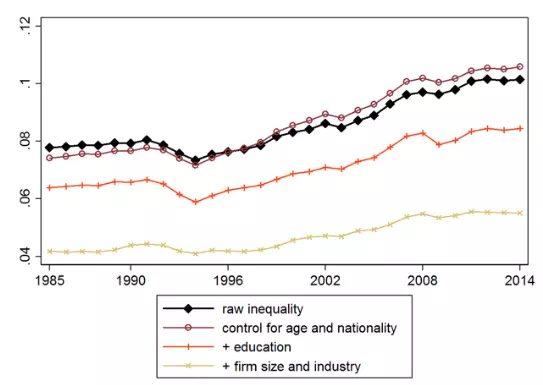
Those geographical wage disparities have grown over time. The black line in Figure 1 depicts the standard deviation in average log wages across 204 West German cities, which is steadily increasing since the mid-1990s. Controlling for various observable characteristics of the local workforce such as age, education, or industry composition reduces the level of spatial wage inequality, but the time trends remain similar. In the most comprehensive specification (see the yellow line) the standard deviation of the average conditional wage distribution has grown by 42% in Germany. This is only slightly smaller than in the US, where a comparable measure across 220 local areas has increased by 48% over the same period (Moretti 2011).
What is behind such large and growing spatial disparities? In a recent paper (Dauth et al. 2018) we argue that one key driver, which has been mostly neglected in the empirical urban economics literature, is rising assortative matching of high-quality workers and plants in large cities.
Positive assortative matching between and within cities drives spatial wage inequality
Our analysis is based on detailed administrative linked employer-employee data that covers the full job history of the universe of private sector workers in (West) Germany during the time period 1985-2014 – about 30 million persons and 2 million establishments per year. We follow Card et al. (2013) and Abowd et al. (1999) to estimate fixed effects for every worker and every plant and then explore (changes in) the spatial distribution of those measures of worker and plant quality.
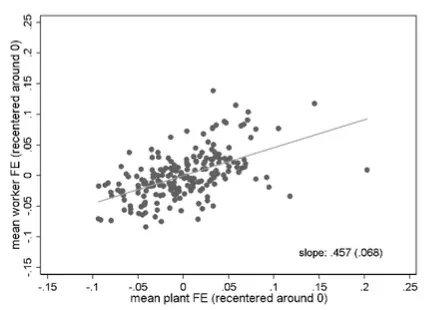
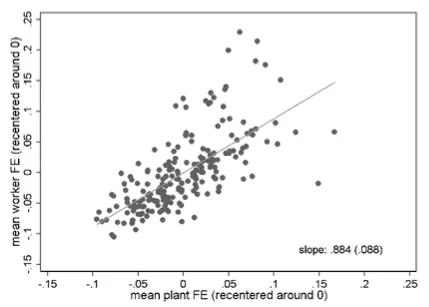
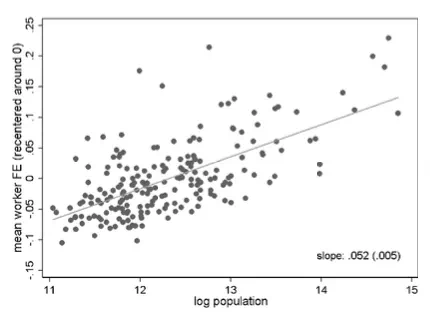
Assortative matching matters in two different ways. First, there is the tendency of high-quality workers and plants to co-locate in the same local labour markets. The top two panels in Figure 2 show the positive relationship between average worker and plant quality across the 204 cities for two separate time windows. The figure suggests that the strength of this co-location pattern almost doubled over time: the elasticity is 0.457 in the period 1985-1991 and 0.884 in 2008-2014. The places were high-quality workers and plants cluster together tend to be the large West German cities like Munich, Hamburg or Frankfurt. This is shown in the bottom two panels of Figure 2 where we find positive associations between local population size and both average quality measures.
Figure 2 Co-location of high-quality workers and plants in large German cities
Co-location of high-quality workers and plants (top: 1985-1991, bottom: 2008-2014)
(Log) population size and average worker quality (top) and average plant quality (bottom), 2008-2014
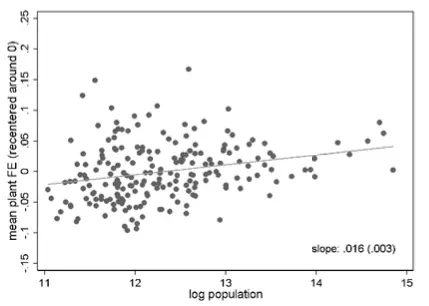
But large cities like Munich do not only exhibit increasingly better pools of workers and plants than small cities like Uelzen. The second key mechanism is stronger assortative matching within those local labour markets. Inside Munich, matches are formed where the qualities of employers and employees are tightly aligned. The relatively best-paid persons tend to work for the relatively best paying local firms. Within Uelzen, by contrast, matching is far less assortative; who works for whom is closer to random.
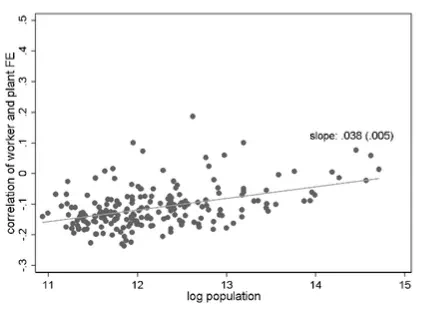
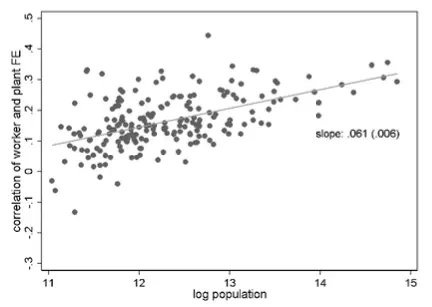
To show this more specifically, we compute the correlation of the worker fixed effects and the corresponding plant fixed effects of their employers in the first year of the respective time window. Figure 3 shows that this correlation tends to be higher in larger cities. Moreover, the association between local labour market size and within-city assortativeness has become considerably stronger over time: the elasticity is 0.038 in the period 1985-1991 and 0.061 in 2008-2014. In other words, job matches in Munich were more assortative than in Uelzen already in 1985-1991, but even more so in 2008-2014. This has contributed considerably to the rising wage gap between Munich and Uelzen.
Figure 3 Stronger assortative matching within large German cities
(Log) population size and within-city correlation of worker and plant qualities, 1985-1991 (top), 2008-2014 (bottom)
Extended analyses in the paper show that a similar pattern arises at a fine-grained level for specific occupations. The chance that, say, a high-quality chemical engineer is matched with a high-quality plant is significantly better in Munich than in Uelzen. The reason is not only that Munich is larger overall, but because the local job market for chemical engineers is thicker than in Uelzen – with more potential employers in the chemical industry and more other chemical engineers.
We also explore some reasons why larger local labour markets facilitate a tighter assortative matching. One reason could be that search costs are lower in larger markets, which implies fewer frictions to fill vacancies. Another reason could be a complementarity effect: when the gains from finding a productive match are increasing in the own quality, large cities naturally provide higher incentives for assortative matching because the pools of workers and firms tend to be of higher quality there.
Quantitative implications
After having documented these new facts, we conduct several counterfactual exercises (under weak parametric assumptions) to gauge the quantitative impact of assortative matching for spatial wage disparities and aggregate earnings in Germany.
In one exercise, we set the strength of within-city matching to zero everywhere. This corresponds to a hypothetical scenario where the pools of workers and plants across cities are as observed in 2014, but where worker-plant matching within all local labour markets is now entirely random. Our simulation shows that the standard deviation of log average wages would indeed be 5% smaller in such a world. But this comes at the cost of substantially lower aggregate earnings. In fact, German workers would lose roughly €26 billion per year in that scenario, because large cities lose their advantage of tight assortative matching which in turn leads to lower urban wages.
In a related thought experiment, we reverse the increasing within-city assortativeness that occurred over the last 30 years. More specifically, we take the pools of workers and plants across cities as observed in 2014, but assume that all local labour markets keep their 1991 degrees how tightly worker and plant qualities are aligned. Again, geographical wage disparities would be 2.5% smaller in that case, had the rise in assortativeness not happened. But aggregate labour earnings would be reduced by €31 billion this time.
Finally, we conduct a thought experiment going into the opposite direction, by imposing perfect assortative matching in all cities. This would trigger ubiquitous (though uneven) wage increases, since matching would improve everywhere, and total labour earnings in Germany would increase by a whopping €84 billion. Matching frictions in local labour markets, therefore, seem to have a first-order impact on the aggregate economy.
Lessons for policy
Policymakers in various countries are becoming increasingly concerned about rising urban-rural labour market divides which arise when top workers and firms increasingly concentrate in large cities. Many countries, including the US and Germany, have therefore adopted ‘place-based policies’ that aim for a reduction of spatial economic disparities.
There are many ways how to design those policies and more much more research is needed to find out which ones work best. One possibility is to subsidise high-quality agents to locate outside big cities. However, such policies can be costly because those workers or firms lose the benefits of tight labour market matching that large cities provide. Moreover, their resettlement has negative externalities on the functioning of urban labour markets and thus imposes aggregate earnings losses.
Our research suggests that a more promising strategy could be to improve matching within small cities. Examples for upgrades of matching technologies could be infrastructure investments, the creation of learning platforms or colleges to facilitate job search, and so on. If small cities could mimic the degree of assortativeness of large cities, this would reduce spatial wage disparities. But it would potentially come at a smaller aggregate cost, or even at aggregate gains, because it raises the productivity of small cities without artificially diverting economic activity to those areas.