Relative Elasticity

Perfectly Elastic and Perfectly Inelastic

To begin the conversation about relative elasticity, it helps to first look at the extremes.

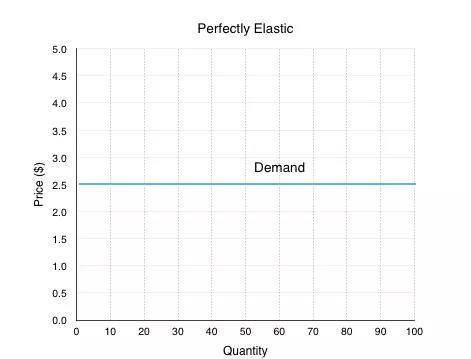
Perfectly Elastic

Imagine a product where if the price increased, even slightly, you wouldn’t buy any it anymore. Sound familiar? That’s because we introduced this concept in Topic 3, as one of the assumptions of a perfectly competitive market. One of the examples we used was identical hot dog stands, side by side, where the only difference was price. If quality is the same, the rational consumer will always purchase the hot dog that is a lower price. From the perspective of the stand, they know that if they increase price even slightly, they will sell 0 units. This means that E_D = ∞.

Using point-slope at any point in Figure 4.3a, we can confirm this.

$Description: \frac{\Delta Q}{\Delta P}\cdot \frac{P}{Q}=?$

We know that $Description: \frac{\Delta Q}{\Delta P}$ is equal to the inverse of the slope. In the demand curve in Figure 4.3a, when the ΔP>0 then ΔQ is equal to ∞. This means that $Description: \frac{\Delta Q}{\Delta P}$ = ∞.

Description: image003

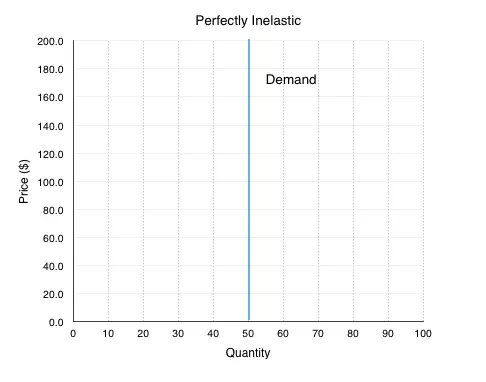
Perfectly Inelastic

At the other end of the spectrum, consider a market where the firm can continue to increase prices with no change in quantity. If you were poisoned and had to buy the antidote, would you be responsive to price change? Probably not. This is an example of a situation where demand is nearly perfectly inelastic. If you increase the price, quantity demanded does not change. This means that E_D = 0.

We can confirm this by using point-slope at any point in Figure 4.4a.

In the demand curve in Figure 4.3a, when the ΔP>0 then ΔQ is equal to 0. This means that $Description: \frac{\Delta Q}{\Delta P}$ = 0.

Description: image004