Producer theory
In this chapter we analyze producerís behavior. This is important to understand
(i) demand for input factors (like capital or labor),
(ii) firmís cost functions, as well as
(iii) technological progress. We start by introducing a standard way of describing technology using production function, discuss important aspects of technology and then define firmís cost and study a cost minimization problem. All of that will be necessary to analyze firmís profit maximization in the following chapters.
Technology and output
Technology transforms inputs (or production factors) into outputs. Examples of inputs include: labor services, physical capital, land, raw materials or intermediate goods, etc. Inputs are goods, so again we shall speak about specific inputs, differentiated not only with respect to physical characteristics, but also location, time or state of the world. Production usually takes time, but if one differentiates goods according to time, our description would be general enough to incorporate timing implicitly. Typically output and inputs are multidimensional: to produce a given good one usually needs many inputs and similarly usually one produces many outputs at the same time (e.g. energy and pollution). At this level we will focus on the examples with a single output and two inputs. Technology is typically summarized using a production function that transforms inputs into a maximal level of output that can be produced from a given combination of inputs. An example of a production function is given by f with values:

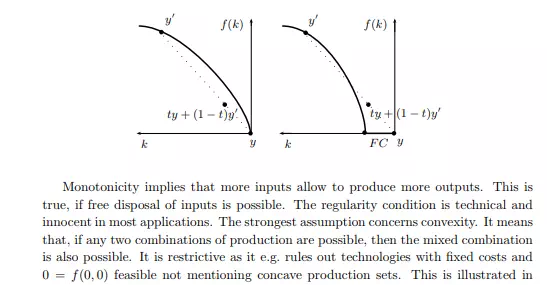
for the example of single input concave production function f without and with fixed costs (F C). We will sometimes dispense with convexity assumption in our analysis.
ē using large scale technologies, i.e. although the single technology may posses constant or decreasing returns to scale at certain production levels, if the scale increases the company may switch to more efficient large scale technologies and actual production data would suggest an increasing returns to scale.
ē few other including: economies of scale in purchases (higher discounts for higher orders) or marketing (higher hit ratio of marketing campaigns of larger firms). Capital intensive technologies usually have increasing returns, while labor intensive constant or decreasing returns. Clearly increasing returns to scale violate convexity assumption. Can you verify that? Replication argument would suggest that, in the worst case scenario the company may e.g. double its production by building a second factory aside, so the constant or increasing returns to scale assumption should be natural. Put differently, we shall not observe decreasing returns to scale in reality. However, there are examples of decreasing returns to scale technologies.
The reason is simple, the returns to scale analysis assumes that all factors can be multiplied proportionally, however, sometimes it is not possible as some factors may be constrained or even fixed (e.g. natural resources available in a give region, or specific job supply in an area, or even communication possibilities, etc.). So typically, when we speak of decreasing returns one should think of fixed (production) factors. Some factors may be fixed in the short run but become flexible in the long run. Specifically, we talk about a short run technology / production function, if one of the factors (like capital) is fixed: q = f( Įk, l), where Įk is some predefined constant. Efficiency requires that for industries with increasing returns to scale we should observe a small number of large firms, while with decreasing returns a large number of small firms.
If both small and large companies may coexists at the same market we could imply that scale does not matter and hence industry exhibits constant returns. The following examples discuss the introduced concepts. See also Douglas (1948) for a seminal development on production functions.