Types of Product Of Sum Forms

There are different types of Product of Sum forms.

·         Canonical POS Form

·         Non – Canonical Form

·         Minimal POS Form

Canonical POS Form

It is also known as Product of Max term or Canonical conjunctive normal form (CCNF). Canonical means standard and conjunctive means intersection.

In this form, Maxterms are AND together for which output is false.

Canonical POS expression is represented by ∏ and Maxterms for which output is false in brackets as shown in the example given below.

F              =             ∏ (M₀, M₄, M₆, M₇)

Expanding the product

F              =             M₀.M₄.M₆.M₇

Putting Max terms

F              =             (A+B+C)(A̅+B+C)(A̅+B̅+C)(A̅+B̅+C̅)

The canonical form contains all inputs either complemented or non-complemented in its each Sum term.

Non – Canonical Form

The product of sum expression that is not in standard form is called non-canonical form.

Let’s take the above-given function as an example.

F              =             (A+B+C)(A̅+B+C)(A̅+B̅+C)(A̅+B̅+C̅)

F              =             (B+C) (A̅+B̅+C)(A̅+B̅+C̅)

Same but inverted terms eliminates from two Max terms and form a single term to prove it here is an example.

= (A+B+C) (A̅+B+C)

= AA̅+AB+AC+A̅B+BB+BC+A̅C+BC+CC

= 0+AB+AC+A̅B+A̅C+B+BC+C

= A(B+C)+A̅(B+C)+B(1+C)+C

= (B+C)(A+A̅)+B(1)+C

= (B+C)(0)+B+C

= B+C

The expression achieved is still in Product of Sum form but it is non-canonical form.

Minimal POS Form

This is the most simplified and optimized form of a POS expression which is non-canonical. Minimal Product of Sum form can be achieved using Boolean algebraic theorems like in the non-canonical example given above. Another method of achieving minimal POS form is by using Karnaugh map which is comparatively easier than using Boolean algebraic theorems.

Minimal POS form uses less number of inputs and logic gates during its implementation, that’s why they are being preferred over canonical form for their compact,fast and low-cost implementation.

Let’s take the above-given function as example

K-map of the function

Minimal expression using K-map

F = (B+C) (A̅+B̅)

The achieved expression is the minimal product of sum form. It is still Product of Sum expression But it needs only 2 inputs two OR gates and a single 2 input AND gate. However, the canonical form needs 4 OR gates of 3 inputs and 1 AND gate of 4 inputs.

·         You may also read: Negative Feedback and Negative Feedback Amplifier Systems

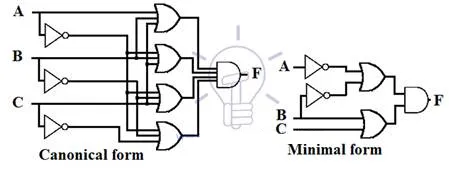
Schematic Design of Product of Sum (POS)

The product of Sum expression has a specific schematic design of OR-AND. In OR-AND the inputs go through an array of OR gates which is the first level of gates, the output of the first level OR gates goes through the second level of the gate,which is an AND gate.

The number of inputs and number of gates used in this design depends upon the expression that is to be implemented.

The canonical form consists of the max number of possible inputs and gates,however, the minimal form consists of the lowest possible number of inputs and gates. The schematic design of canonical and minimal POS form is given below.

Conversion from Minimal POS to Canonical form POS

As we know the canonical form of POS has max terms and max terms contains every input either complemented or non-complemented. So we will add every sum term with the product of complemented and non-complemented missing input. Example of its conversion is given below.

Minimal POS form

                F = (A̅+B̅) (B+C)

(A̅+B̅) term is missing C input so we will add (CC̅) with it. (B+C) term is missing A input so we will add (AA̅) with it.

                F = (A̅+B̅+CC̅) (B+C+AA̅)

                F = (A̅+B̅+C)(A̅+B̅+C̅)(A+B+C)(A̅+B+C)

This expression is now in canonical form.

Conversion From Canonical POS to SOP

The product of Sum expression can be converted into Sum of Product form only if the expression is in canonical form. Canonical POS and canonical SOP are inter-convertible i.e. they can be converted into one another.  Example of POS to SOP conversion is given below.

POS canonical form

                F = (A+B+C)(A̅+B+C)(A̅+B̅+C)(A̅+B̅+C̅)

In canonical form each sum term is a max term so it can also be written as:

                F = ∏(M₀,M₄,M₆,M₇)

The remaining combinations of inputs are minterms of the function for which its output is true. To convert it into SOP expression first we will change the symbol to summation (∑) and use the remaining minterm.

                F = ∑ (m₁,m₂,m₃,m₅)

Now we will expand the summation sign to form canonical SOP expression.

                F = A̅B̅C + A̅BC̅ + A̅BC + AB̅C

Min terms are complement of Max terms for the same combination of inputs.

Canonical to Minimal POS

A canonical Product of Sum expression can be converted into Minimal Product of sum form by using Karnaugh map (K-map). Another method for converting canonical into minimal is by using Boolean algebraic theorems.

The use of K-map is very easy that is why K-map is preferred. For minimal POS expression, 0’s in K-map are combined into groups and the expression we get is complemented since the groups were made of ‘0’s. Its example has been done above.