Types of Sum Of Product (SOP) Forms

There are few different forms of Sum of Product.

·         Canonical SOP Form

·         Non-Canonical SOP Form

·         Minimal SOP Form

Canonical SOP Form

This is the standard form of Sum of Product. It is formed by O Ring the minterms of the function for which the output is true. This is also known as Sum of Min terms or Canonical disjunctive normal form (CDNF). It is just a fancy name. “canonical” means “standardized” and “disjunctive” means “Logical OR union”.

Canonical SOP expression is represented by summation sign ∑ and minterms in the braces for which the output is true.

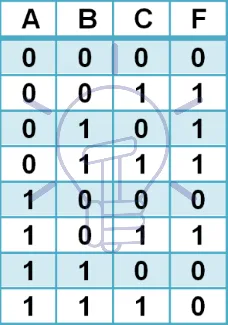
For example, a functions truth table is given below.

For this function the canonical SOP expression is

F = ∑( m₁, m₂, m₃, m₅ )

Which means that the function is true for the min terms {1, 2, 3, 5}.

By expanding the summation we get.

F = m₁ + m₂ + m₃ + m₅

Now putting min terms in the expression

F = A̅B̅C + A̅BC̅ + A̅BC + AB̅C

Canonical form contains all inputs either complemented or non-complemented in its product terms.

You may also read: Digital Synchronous Counter – Types, Working & Applications

Non-Canonical SOP Form

As the name suggests, this form is the non-standardized form of SOP expressions. The product terms are not the min terms but they are simplified. Let’s take the above function in canonical form as an example.

F = A̅B̅C + A̅BC̅ + A̅BC + AB̅C

F = A̅B̅C + A̅B(C̅ + C) + AB̅C

F = A̅B̅C + A̅B(1) + AB̅C

F = A̅B̅C + A̅B + AB̅C

This expression is still in Sum of Product form but it is non-canonical or non-standardized form.

Minimal SOP Form

This form is the most simplified SOP expression of a function. It is also a form of non-canonical form. Minimal SOP form can be made using Boolean algebraic theorems but it is very easily made using Karnaugh map (K-map).

Minimal SOP form is preferred because it uses the minimum number of gates and input lines. it is commercially beneficial because of its compact size, fast speed, and low fabrication cost.

Let’s take an example of the function given above in canonical form.

Its K-map is given below.

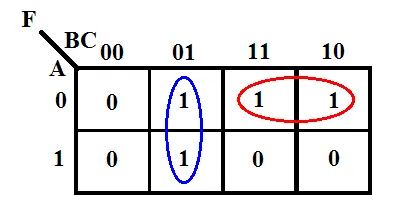
According to the K-map, the output expression will be

F = B̅C + A̅B

This is the most simplified & optimized expression for the said function. This expression requires only two 2-input AND gates & one 2-input OR gate. However, the canonical form needs four 3-input AND gates & one 4-input OR gate, which is relatively more costly than minimal form implementation.

·         You may also read: Ring Counter & Johnson Counter – Construction & Operation

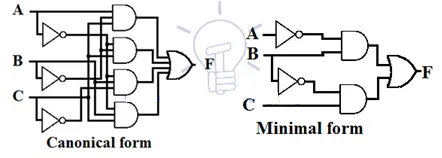
Schematic Design of Sum Of Product (SOP)

SOP expression implements 2 level AND-OR design in which the 1^st level gate is AND gate following the 2^nd level gate which is OR gate. Schematic design of SOP expression needs a group array of AND gates & one OR gate.

Every SOP expression has somewhat same designing i.e. all the inputs goes through AND gate and then the output of these AND gates flow through an OR gate as shown in the figure given below.

The number of inputs and the number of AND gates depend upon the expression one is implementing.

Example of designs of canonical and minimal SOP expression for a function is given below.

Conversion from Minimal SOP to Canonical SOP Form

Conversion from minimal or any sort of non-canonical form to canonical form is very simple.

As we know canonical form has min terms & min terms consists of all inputs either complemented or non-complemented. So we will multiply every term of minimal SOP with the sum of missing input’s complemented and non-complemented form. Example of conversion for the above function in minimal SOP form is given below.

Minimal SOP form

F = A̅B + B̅C

The term A̅B is missing input C. So we will multiply A̅B with (C+C̅) because (C+C̅ = 1). The term B̅C is missing input A. so it will be multiplied with (A+A̅)

F = A̅B(C + C̅) + B̅C(A + A̅)

F = A̅BC + A̅BC̅ + AB̅C + A̅B̅C

Now, this expression is in canonical form.