Construction of Combinational Circuits

A Combinational Circuit consist of logic gates whose outputs at any instant of time are determined directly from the present combination of inputs without regard to previous input. Examples of combinational circuits: Adder, Subtractor, Converter, and Encoder/Decoder.

Here we are going to learn how to construct and analyze any type of combinational circuit using four general steps. I am going to explain this trick with the help of the one combinational circuit and you can apply the same for implementing other combinational circuits.

Following are the four steps to construct and analyze any combinational circuit.

·         Step-1: Identify the number of inputs and outputs of the circuit.
First of all, we have to think about the inputs and outputs of the circuit by considering which type of logical operation we want to perform with the circuit.
For example, we have to create a circuit that can add two bits. For this, we require two inputs (one for the first bit (A) another for the second bit (B)) and two outputs one for sum (S) of two bits and another for carry (C).

In total, we require 2 inputs and 2 outputs. So here our first step is completed.

·         Step-2: Creating the Truth Table.
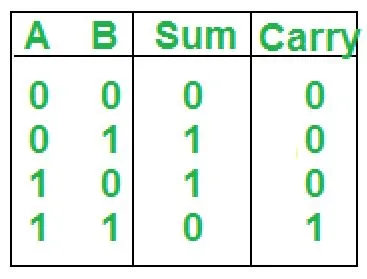
In this step we have to create truth table for our circuit so for this first we will create input columns and list all the possible combinations of inputs. In our case 2 bits can have maximum 4 combinations (00 01 10 11).
Now in output, we have two columns (Sum and Carry) as discussed earlier. Now we have to fill output columns in such a way that for which logical operation we are constructing circuit.

In our circuit, we want addition so we will add those input bits and write the sum of those bits in (Sum) column and if carry is generated we will write 1 else write.

0 in (Carry) column.

·         Step-3: Simplify the Boolean function for each output.
In this step, we have to just create a simplified Boolean function according to inputs and outputs of the truth table obtained in the previous step.
For Sum,

Sum = A'B + AB' = A XOR B

For Carry,

Carry = AB = A AND B

·         Step-4: Constructing circuit using Boolean function obtained from third step.
For sum, we have obtained (A XOR B) so we will connect A and B to the inputs of XOR gate and take its output as a sum. For carry, we have obtained (A AND B) so we will connect A and B to the inputs of AND gate and take its output as a carry.

Now in this circuit, if you provide input at A and B ends. You will get the output on sum and carry ends according to truth table we have created above. So here we have completed our four steps for creating the combinational circuit.