Digital Circuits - De-Multiplexers
De-Multiplexer is a combinational circuit that performs the reverse operation of Multiplexer. It has single input, ‘n’ selection lines and maximum of 2noutputs. The input will be connected to one of these outputs based on the values of selection lines.
Since there are ‘n’ selection lines, there will be 2n possible combinations of zeros and ones. So, each combination can select only one output. De-Multiplexer is also called as De-Mux.
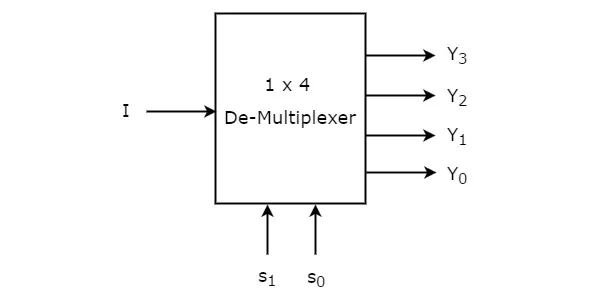
1x4 De-Multiplexer
1x4 De-Multiplexer has one input I, two selection lines, s1 & s0 and four outputs Y3, Y2, Y1 &Y0. The block diagram of 1x4 De-Multiplexer is shown in the following figure.

The single input ‘I’ will be connected to one of the four outputs, Y3 to Y0 based on the values of selection lines s1 & s0. The Truth table of 1x4 De-Multiplexer is shown below.
Selection Inputs | Outputs | ||||
S1 | S0 | Y3 | Y2 | Y1 | Y0 |
0 | 0 | 0 | 0 | 0 | I |
0 | 1 | 0 | 0 | I | 0 |
1 | 0 | 0 | I | 0 | 0 |
1 | 1 | I | 0 | 0 | 0 |
From the above Truth table, we can directly write the Boolean functions for each output as
Y3=s1s0IY3=s1s0I
Y2=s1s0′IY2=s1s0′I
Y1=s1′s0IY1=s1′s0I
Y0=s1′s0′IY0=s1′s0′I
We can implement these Boolean functions using Inverters & 3-input AND gates. The circuit diagram of 1x4 De-Multiplexer is shown in the following figure.
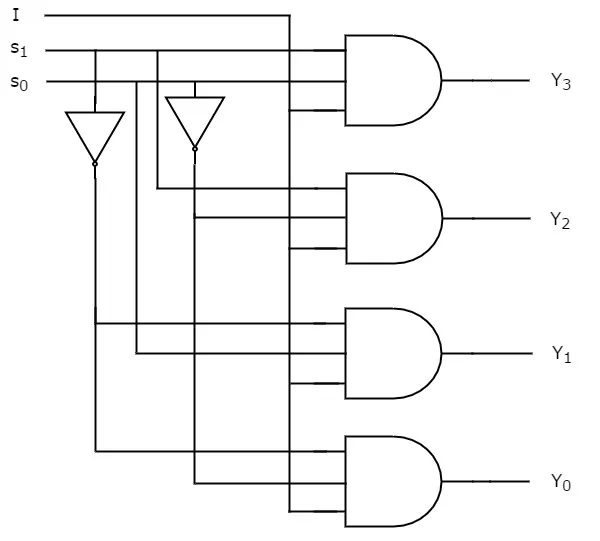
We can easily understand the operation of the above circuit. Similarly, you can implement 1x8 De-Multiplexer and 1x16 De-Multiplexer by following the same procedure.
Implementation of Higher-order De-Multiplexers
Now, let us implement the following two higher-order De-Multiplexers using lower-order De-Multiplexers.
1x8 De-Multiplexer
In this section, let us implement 1x8 De-Multiplexer using 1x4 De-Multiplexers and 1x2 De-Multiplexer. We know that 1x4 De-Multiplexer has single input, two selection lines and four outputs. Whereas, 1x8 De-Multiplexer has single input, three selection lines and eight outputs.
So, we require two 1x4 De-Multiplexers in second stage in order to get the final eight outputs. Since, the number of inputs in second stage is two, we require 1x2 DeMultiplexer in first stage so that the outputs of first stage will be the inputs of second stage. Input of this 1x2 De-Multiplexer will be the overall input of 1x8 De-Multiplexer.
Let the 1x8 De-Multiplexer has one input I, three selection lines s2, s1 & s0 and outputs Y7 to Y0. The Truth table of 1x8 De-Multiplexer is shown below.
Selection Inputs | Outputs | |||||||||
s2 | s1 | s0 | Y7 | Y6 | Y5 | Y4 | Y3 | Y2 | Y1 | Y0 |
0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | I |
0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | I | 0 |
0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | I | 0 | 0 |
0 | 1 | 1 | 0 | 0 | 0 | 0 | I | 0 | 0 | 0 |
1 | 0 | 0 | 0 | 0 | 0 | I | 0 | 0 | 0 | 0 |
1 | 0 | 1 | 0 | 0 | I | 0 | 0 | 0 | 0 | 0 |
1 | 1 | 0 | 0 | I | 0 | 0 | 0 | 0 | 0 | 0 |
1 | 1 | 1 | I | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
We can implement 1x8 De-Multiplexer using lower order Multiplexers easily by considering the above Truth table. The block diagram of 1x8 De-Multiplexer is shown in the following figure.
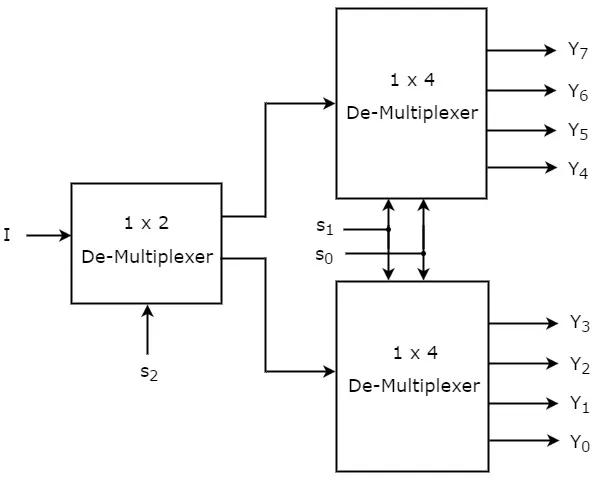
The common selection lines, s1 & s0 are applied to both 1x4 De-Multiplexers. The outputs of upper 1x4 De-Multiplexer are Y7 to Y4 and the outputs of lower 1x4 De-Multiplexer are Y3 to Y0.
The other selection line, s2 is applied to 1x2 De-Multiplexer. If s2 is zero, then one of the four outputs of lower 1x4 De-Multiplexer will be equal to input, I based on the values of selection lines s1 & s0. Similarly, if s2 is one, then one of the four outputs of upper 1x4 DeMultiplexer will be equal to input, I based on the values of selection lines s1 & s0.
1x16 De-Multiplexer
In this section, let us implement 1x16 De-Multiplexer using 1x8 De-Multiplexers and 1x2 De-Multiplexer. We know that 1x8 De-Multiplexer has single input, three selection lines and eight outputs. Whereas, 1x16 De-Multiplexer has single input, four selection lines and sixteen outputs.
So, we require two 1x8 De-Multiplexers in second stage in order to get the final sixteen outputs. Since, the number of inputs in second stage is two, we require 1x2 DeMultiplexer in first stage so that the outputs of first stage will be the inputs of second stage. Input of this 1x2 De-Multiplexer will be the overall input of 1x16 De-Multiplexer.
Let the 1x16 De-Multiplexer has one input I, four selection lines s3, s2, s1 & s0and outputs Y15 to Y0. The block diagram of 1x16 De-Multiplexer using lower order Multiplexers is shown in the following figure.
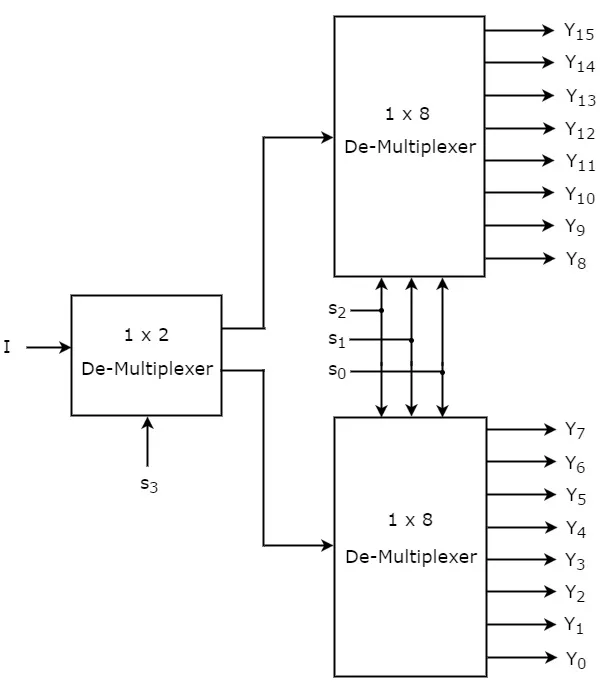
The common selection lines s2, s1 & s0 are applied to both 1x8 De-Multiplexers. The outputs of upper 1x8 De-Multiplexer are Y15 to Y8 and the outputs of lower 1x8 DeMultiplexer are Y7 to Y0.
The other selection line, s3 is applied to 1x2 De-Multiplexer. If s3 is zero, then one of the eight outputs of lower 1x8 De-Multiplexer will be equal to input, I based on the values of selection lines s2, s1 & s0. Similarly, if s3 is one, then one of the 8 outputs of upper 1x8 De-Multiplexer will be equal to input, I based on the values of selection lines s2, s1 & s0.