Number conversion Algorithms

CS Principles

This activity introduces the concept that abstractions built upon binary sequences can be used to represent all digital data . It also introduces the concept of an algorithm. It focuses on the following learning objectives:

5b. Explanation of how number bases, including binary and decimal, are used for reasoning about digital data.
16a. Use of natural language, pseudo-code, or a visual or textual programming language to express an algorithm.

Introduction

This lesson assumes you have completed the homework on binary and hexadecimal number systems. That homework decribed how the binary, decimal, and hexadecimal number systems work and showed how to convert from one number system to another.

In this lesson we want generalize what we learned their by seeing those number systems as specific examples of a more general concept, a positional number system.

We will develop algorithms that will enable you to perform conversions from one number system to another.

The type of generalization we are doing in this lesson is another example of the abstraction principle in computer science -- here we are focusing on a general pattern that holds true for all positional number systems.

Algorithms and Pseudocode

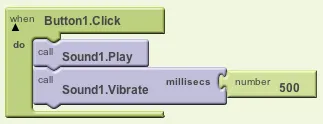
An algorithm is a step-by-step procedure to perform some computation. For example, the steps you take in the Hello Purr app when the button is clicked is an example of a simple 2-step algorithm:

To help us talk about algorithms we will use pseudocode, a language or notation that has many of the structures of a programming language but is easy to read. Pseudocdes are halfway between natural languages like English and formal programming languages.

Positional Number Systems

Let's review some of the key points that you learned in the Khan Academy videos.

Our decimal number system (and the binary and hexadecimal systems) are particular instances of the more general concept of a positional number system.
In a positional number system the same symbol can represent different values depending on its position (or place) in the numeral. For example, in 91, the 9 represents 90 (the 10s place) but in 19 it represents 9 (the ones place). Contrast this with how symbols work in a non-positional system, like Roman numerals, where X always represents 10.
The base of a number system represents the number of symbols it has:

Name	Base	Symbols
Decimal	10	0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Binary	2	0, 1
Hexadecimal	16	0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
Octal	8	0, 1, 2, 3, 4, 5, 6, 7

Positional number systems use exponentiation to determine a symbol's value based on its place. We can use this idea to convert from any system into the decimal system:

System	Base	Value	Conversion Formula	Decimal Value
Decimal	10	104	(1 × 10²) + (0 × 10¹) + (4 × 10⁰)	100 + 0 + 4 = 104
Binary	2	111	(1 × 2²) + (1 × 2¹) + (1 × 2⁰)	4 + 2 + 1 = 7
Octal	8	104	(1 × 8²) + (0 × 8¹) + (4 × 8⁰)	64 + 0 + 4 = 68
Hexadecimal	16	FEC	(F × 16²) + (E × 16¹) + (C × 8⁰)	15 × 256 + 14 × 16 + 12 × 1 = 3840 + 224 + 12 = 4076

Conversion Algorithms

Let's summarize these conversion formulas by developing an general algorithm that will convert from any base into decimal.

Algorithm to Convert From Any Base to Base 10 Decimal

Let n be the number of digits in the number. For example, 104 has 3 digits, so n=3.
Let b be the base of the number. For example, 104 is decimal so b = 10.
Let s be a running total, initially 0.
For each digit in the number, working left to right do:
Subtract 1 from n.
Multiply the digit times bⁿ and add it to s.
When your done with all the digits in the number, its decimal value will be s

Let's try it on the binary number 1011.

Let n = 4.

Let b = 2.

Let s = 0.

First digit, 1: n = 3, 1 × bⁿ is 1 × 2³ = 8. So s = 8.

Second digit, 0: n = 2, 0 × bⁿ is 0 × 2² = 0. So s = 8.

Third digit, 1: n = 1, 1 × bⁿ is 1 × 2¹ = 2. So s = 10

Last digit, 1: n = 0, 1 × bⁿ is 1 × 2⁰ = 1. So 1011₂ = 11₁₀

Digit	n	Value = Digit * bⁿ	Running Total
1	3	1 × 2³ = 8	8
0	2	0 × 2² = 0	8
1	1	1 × 2¹ = 2	10
1	0	1 × 2⁰ = 1	11

Let's try it on the hex number 7E.

Let n = 2.

Let b = 16.

Let s = 0.

First digit, 7: n = 1, 7 × bⁿ is 7 × 16¹ = 7 × 16 = 112. So s = 112.

Last digit, E: n = 0, 14 × bⁿ is 14 × 16⁰ = 14. So s = 112 + 14 = 126. So 7E₁₆ = 126₁₀

Digit	n	Value = Digit * bⁿ	Running Total
7	1	7 × 16¹ = 112	114
E	0	14 × 16⁰ = 14	126

Let's try it on the octal number 124.

Let n = 3.

Let b = 8.

Let s = 0.

First digit, 1: n = 2, 1 × bⁿ is 1 × 8² = 1 × 64 = 64. So s = 64.

Second digit, 2: n = 1, 2 × bⁿ is 2 × 8¹ = 2 × 8 = 16. So s = 64 + 16 = 80.

Last digit, 4: n = 0, 4 × bⁿ is 4 × 8⁰ = 4. So s = 80 + 4 = 84. So 124₈ = 84₁₀

Digit	n	Value = Digit * bⁿ	Running Total
1	2	1 × 8² = 64	64
2	1	2 × 8¹ = 16	80
4	0	4 × 8⁰ = 4	84

Algorithm to Convert From Decimal To Another Base

Let n be the decimal number.
Let m be the number, initially empty, that we are converting to. We'll be composing it right to left.
Let b be the base of the number we are converting to.
Repeat until n becomes 0
   Divide n by b, letting the result be d and the remainder be r.
   Write the remainder, r, as the leftmost digit of b.
   Let d be the new value of n.

Let's use the algorithm to convert 45 into binary.

Let n = 45.

Let b = 2.

Repeat

45 divided by b is 45/2 = 22 remainder 1. So d=22 and r=1. So m= 1 and the new n is 22.

22 divided by b is 22/2 = 11 remainder 0. So d=11 and r=1. So m= 01 and the new n is 11.

11 divided by b is 11/2 = 5 remainder 1. So d=5 and r=1. So m= 101 and the new n is 5.

5 divided by b is 5/2 = 2 remainder 1. So d=2 and r=1. So m= 1101 and the new n is 2.

2 divided by b is 2/2 = 1 remainder 0. So d=1 and r=0. So m= 01101 and the new n is 1.

1 divided by b is 1/2 = 0 remainder 1. So d=0 and r=1. So m=101101 and the new n is 0. So 45₁₀ = 101101₂

Let's use it to convert 99 into binary.

Let n = 99.

Let b = 2.

Repeat

99 divided by b is 99/2 = 49 remainder 1. So d=49 and r=1. So m= 1 and the new n is 49.

49 divided by b is 49/2 = 24 remainder 1. So d=24 and r=1. So m= 11 and the new n is 24.

24 divided by b is 24/2 = 12 remainder 0. So d=12 and r=0. So m= 011 and the new n is 12.

12 divided by b is 12/2 = 6 remainder 0. So d=6 and r=0. So m= 0011 and the new n is 6.

6 divided by b is 6/2 = 3 remainder 0. So d=3 and r=0. So m= 00011 and the new n is 3.

3 divided by b is 3/2 = 1 remainder 1. So d=1 and r=1. So m= 100011 and the new n is 1.

1 divided by b is 1/2 = 0 remainder 1. So d=0 and r=1. So m=1100011 and the new n is 0. So 99₁₀ = 1100011₂

Let's use it to convert 45 into hexadecimal.

Let n = 45.

Let b = 16.

Repeat

45 divided by b is 45/16 = 2 remainder 13. So d=2 and r=13. So m= D and the new n is 2.

2 divided by b is 2/16 = 0 remainder 2. So d=0 and r=2. So m=2D and the new n is 0. So 45₁₀ = 2D₁₆.

Let's use it to convert 99 into hexadecimal.

Let n = 99.

Let b = 16.

Repeat

99 divided by b is 99/16 = 6 remainder 3. So d=6 and r=3. So m= 3 and the new n is 6.

6 divided by b is 6/16 = 0 remainder 6. So d=0 and r=6. So m=63 and the new n is 0. So 99₁₀ is 63₁₆.