Complementation

Truth table for logical AND (.) operator.OR andAND are binary operations because they operate on two variables. Complementation is a unary operation defined on a single variable.

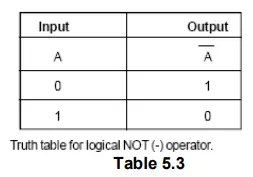
The symbol ‘-‘ is used for complementation operator. It is also known as ‘NOT’ operator. Hence, we write A meaning “complement” of A”, or (A + B) meaning of A + B.” Complementation of a variable is the reverse of its value. Hence, if A = 0, the A= 1 and if A = 1. Then A= 0. Below table 5.3 shows the truth table for logical NOT (-) operator. Ais read as “complement of A” or “not of A”.

Operator Precedence Does A + B .C mean (A + B) . C or A + (B . C)? The two generate different values for A = 1, B = 0, and C = 0 because we have (1 + 0) . 0 = 0 and 1 + (0.0) = 1. Hence, operator precedence rules are needed to correctly evaluate Boolean expressions. The precedence rules for Boolean operators are as follows:

1. The expression is scanned from left to right.

2. Expression enclosed within parentheses are evaluated first.

3. All complement (NOT) operations are performed next.

4. All ‘-‘(AND) operations are performed after that.

5. Finally, all ‘+’(OR) operations are performed in the end.

According to these rules, A + B. C should be evaluated as A + (B .C). Similarly, for the expression A. B, complement of Aand B are both evaluated first and the results are then AND ed. Again, for the expression (A + B), the expression inside the parenthesis (A + B) is evaluated first and the result is then complemented.

Principle of Duality

v When value and operations can be paired up in a way that leaves everything important unchanged when all pairs are switched simultaneously, we call the member of each pair dual to each other. Thus 0 and 1 are dual, ^ and are dual. The duality principle asserts that Boolean. Algebra is unchanged, when all dual pairs are interchanged

v Dual of one expression is obtained by replacing AND (.) with OR (+) and OR with AND together with replacement of 1 with 0 and 0 with 1.