Rigid Pavement Response
Rigid pavements respond to loading in a variety of ways that affect performance (both initial and long-term). The three principal responses are:
- Curling stress. Differences in temperature between the top and bottom surfaces of a PCCslab will cause the slab to curl. Since slab weight and contact with the base restrict its movement, stresses are created.
- Load stress. Loads on a PCC slab will create both compressive and tensile stresses within the slab and any adjacent one (as long as load transfer efficiency is > 0).
- Shrinkage and expansion. In addition to curling, environmental temperatures will cause PCC slabs to expand (when hot) and contract (when cool), which causes joint movement.
These three principal responses typically determine PCC slab geometry (typically described by slab thickness and joint design). As slabs get longer, wider and thinner, these responses, or a combination of them, will eventually exceed the slab’s capacity and cause failure in the form of slab cracking, joint widening or blowup. Note that additional issues, notably load transfer stresses and deflections, must also be accounted for in design.
There are a variety of ways to calculate or at least account for these responses in design. The empirical approach uses the AASHO Road Test results to correlate measurable parameters (such as slab depth and PCC modulus of rupture) and derived indices (such as the load transfer coefficient and pavement serviceability index) to pavement performance. The mechanistic-empirical approach relates calculated pavement stresses to empirically derived failure conditions.
Stress
The stresses of primary concern are associated with slab bending either due to temperature gradients, loading or a combination thereof.
Curling
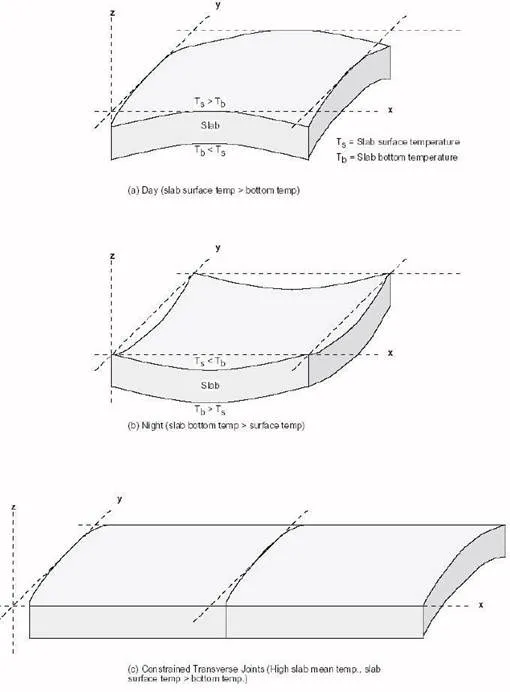
Since PCC is much stronger in compression than tension, tensile stresses tend to control PCC pavement design. Therefore, slab curling calculations seek to find the points of maximum tensile stress as the slab curls due to temperature gradients within (Figure 1). In 1935, measurements reported by Teller and Southerland of the Bureau of Public Roads showed that the maximum temperature differential (hence, maximum curling and maximum tensile stresses) is much larger during the day than during the night. Therefore, the daytime curling stresses are usually most limiting.
To evaluate the tensile warping stresses which develop in the slab, the temperatures at the top and bottom of the slab must be estimated. The first formulas used to estimate warping stresses were developed by Bradbury (1938[1]):
![]()
|
|
|||
|
where: |
st |
= |
slab edge warping stress |
|
C |
= |
coefficient which is a function of slab length and the radius of relative stiffness (shown in Figure 2) |
|
|
E |
= |
modulus of elasticity of PCC |
|
|
e |
= |
thermal coefficient of PCC (» 0.000005/°F) |
|
|
Δ T |
= |
temperature differential between the top and bottom of the slab |
|
For interior stresses, Bradbury’s formula is

|
|
|||
|
where: |
st |
= |
slab interior warping stress |
|
E |
= |
modulus of elasticity of PCC |
|
|
e |
= |
thermal coefficient of PCC (» 0.000005/°F) |
|
|
Δ T |
= |
temperature differential between the top and bottom of the slab |
|
|
C1 |
= |
coefficient in direction of calculated stress |
|
|
C2 |
= |
coefficient in direction perpendicular to C1 |
|
|
m |
= |
Poisson’s ratio for PCC (» 0.15) |
|

Figure 2. Curve showing variation in the differential temperature stress coefficient C for different values of the ratio B/l (redrawn from Bradbury, 1938).
Bradbury also developed an approximate formula for slab corner warping stresses

|
|
|||
|
where: |
st |
= |
slab interior warping stress |
|
E |
= |
modulus of elasticity of PCC |
|
|
e |
= |
thermal coefficient of PCC (» 0.000005/°F) |
|
|
Δ T |
= |
temperature differential between the top and bottom of the slab |
|
|
m |
= |
Poisson’s ratio for PCC (» 0.15) |
|
|
a |
= |
radius of wheel load distribution for corner loading |
|
|
l |
= |
radius of relative stiffness |
|
The radius of relative stiffness (the relative stiffness of the slab relative to that of the foundation) is required for the above formulae. This equation is (from Westergaard, 1926[2]):

|
|
|||
|
where: |
l |
= |
radius of relative stiffness |
|
E |
= |
modulus of elasticity of PCC |
|
|
h |
= |
slab thickness |
|
|
k |
= |
modulus of subgrade reaction |
|
|
m |
= |
Poisson’s ratio for PCC (» 0.15) |
|
Load
The original equations developed by Westergaard (1926[2]) for three critical load locations will be presented. The critical load locations are (after Bradbury, 1938[1] and Westergaard, 1926[2]):
- Interior loading. Occurs
when a load is applied on the interior of a slab surface which is “remote”
from all edges.

- Edge loading. Occurs
when a load is applied on a slab edge “remote” from a slab corner.

- Corner loading. Occurs
when the center of a load is located on the bisector of the corner angle.

Assuming a poisson’s ratio = 0.15, Westergaard’s original equations are:
· Interior loading (tensile stress at the slab bottom)
· Edge loading (tensile stress at the slab bottom)
· Corner loading (tensile stress at slab top)
|
|
||||
|
where: |
σi, σe, σc |
= |
maximum stress (psi) for in interior, edge and corner loadings, respectively |
|
|
W |
= |
wheel load (lbs.) |
||
|
h |
= |
slab thickness (inches) |
||
|
a |
= |
radius of wheel contact area (inches) |
||
|
l |
= |
radius of relative stiffness (inches) |
||
|
b |
= |
radius of resisting section (inches) = |
||
Note that all three equations involved the depth of slab (h) squared. This suggests that slab thickness is very critical in reducing load stresses to acceptable levels.
Shrinkage and Expansion
Although slab shrinkage and expansion causes internal stress, especially as the PCC sets and hardens, the long term concern centers on the joint movement that this shrinkage/expansion can cause. The following formula can be used to estimate joint movement in PCC slabs (FHWA, 1989[3]):
![]()
|
|
|||
|
where: |
z |
= |
joint opening = change in slab length (inches) |
|
C |
= |
base/slab frictional restraint factor |
|
|
L |
= |
slab length (inches) |
|
|
e |
= |
thermal coefficient of PCC (listed by coarse aggregate type) |
|
|
= |
6.6 x 10-6/°F (quartz) |
||
|
= |
6.5 x 10-6/°F (sandstone) |
||
|
= |
6.0 x 10-6/°F (gravel) |
||
|
= |
5.3 x 10-6/°F (granite) |
||
|
= |
4.8 x 10-6/°F (basalt) |
||
|
= |
3.8 x 10-6/°F (limestone) |
||
|
ΔT |
= |
the maximum temperature range (for some cases it is the temperature of the PCC at the time of placement minus the average daily minimum temperature in January) (°F) |
|
|
δ |
= |
shrinkage coefficient of PCC |
|
|
~ |
0.0008 in./in. for indirect tensile strength of 300 psi or less |
||
|
~ |
0.00045 in./in. for indirect tensile strength of 500 psi |
||
|
~ |
0.0002 in./in. for indirect tensile strength of 700 psi or greater |
||
|
(Note: δ should be omitted for rehabilitation projects as shrinkage (assuming no new slab PCC) is not a factor.) |
|||