Construction of the Residue Curve

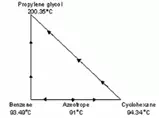
Equation 3 and 4 were used to sketch the corresponding residue curve for the three species. From the above information, we know that these species have boiling points at 94.34 (cyclohexane), 93.49 (benzene) and 200.35^oC (propylene glycol) at the pressure of 150 kPa, and an azeotrope that boils at 91 ^°C between the two more volatile species. As were shown from Figure 6 and Figure 7 there were no new azeotropes formed between the solvent 1,2-propanediol respectively with the another two component in the feed.

Feed Stream Molar Flow Rate (kg mol/h)	Â
Hydrogen	 0.914
Cyclohexane	 159.447
Benzene	 194.944
n-Hexane	 0.127
Total	 355.43
Solvent Stream (Aniline) molar flow rate (kg mol/h)	Â 3600
Solvent/Feed (S/F) ratio	10.13
Distillate Product Molar Flow Rate (kg mol/hr)	Â
Hydrogen	 0.914
Cyclohexane	 158.75
Benzene	 0.075
n-Hexane	 0.127
1,2 propanediol / propylene glycol	 0.004
Total	 159.87
Mole % Composition in the Distillate Product	Â
Hydrogen	 0.571
Cyclohexane	 99.30
Benzene	 0.047
n-Hexane	 0.079
1,2 propanediol / propylene glycol	 0.003
 Total	 1.000

Â

We then start to sketch our residue curve map by sketching the triangular diagram in Figure 8, and placing the arrows pointing from the lower to higher temperatures around the edge. The corner points for benzene and cyclohexane are single species point, and both are unstable nodes - all residue curves leave. The corner point for propylene glycol is a single species point which is a stable node - all residue curve enter. All three are nodes; none are saddles, thus;

N₁ = 3 and S₁ = 0

We then further assume that there will be no ternary azeotrope been form among the three constituents, i.e.,

N₃ = S₃ = 0Â

Figure 6: x-y Plot for Benzene and Propylene Glycol	Figure 7: x-y Plot for Cyclohexane and Propylene Glycol

Â

Figure 8: Preliminary Sketch for Residue Curve

The remaining steps here require the identification of the only binary azeotrope that form between benzene and cyclohexane, to be either a node or a saddle point. From equation 4:

4(0-0) + 2(N₂ - S₂) + (3-0) = 1

2(N₂ - S₂) = -2

N₂ - S₂ = -1

Thus, the only way we can satisfy the above equation is letting N₂ = 0 and S₂ = 1, i.e. the binary azeotrope is a saddle point, which directs the trajectories in another direction.

Â

Figure 9: Completed Sketch for Residue Curve