Particulate Solids

The behaviour of fluids, both liquids and gases is considered, with particular reference to their flow properties and their heat and mass transfer characteristics. Once the composition, temperature and pressure of a fluid have been specified, then its relevant physical properties, such as density, viscosity, thermal conductivity and molecular diffusivity, are defined. In the early chapters of this volume consideration is given to the properties and behaviour of systems containing solid particles. Such systems are generally more complicated, not only because of the complex geometrical arrangements which are possible, but also because of the basic problem of defining completely the physical state of the material.

The three most important characteristics of an individual particle are its composition, its size and its shape. Composition determines such properties as density and conductivity, provided that the particle is completely uniform. In many cases, however, the particle is porous or it may consist of a continuous matrix in which small particles of a second material are distributed. Particle size is important in that this affects properties such as the surface per unit volume and the rate at which a particle will settle in a fluid. A particle shape may be regular, such as spherical or cubic, or it may be irregular as, for example, with a piece of broken glass. Regular shapes are capable of precise definition by mathematical equations. Irregular shapes are not and the properties of irregular particles are usually expressed in terms of some particular characteristics of a regular shaped particle. Large quantities of particles are handled on the industrial scale, and it is frequently necessary to define the system as a whole. Thus, in place of particle size, it is necessary to know the distribution of particle sizes in the mixture and to be able to define a mean size which in some way represents the behaviour of the particulate mass as a whole.  Important operations relating to systems of particles include storage in hoppers, flow through orifices and pipes, and metering of flows. It is frequently necessary to reduce the size of particles, or alternatively to form them into aggregates or sinters. Sometimes it may be necessary to mix two or more solids, and there may be a requirement to separate a mixture into its components or according to the sizes of the particles. In some cases the interaction between the particles and the surrounding fluid is of little significance, although at other times this can have a dominating effect on the behaviour of the system. Thus, in filtration or the flow of fluids through beds of granular particles, the characterisation of the porous mass as a whole is the principal feature, and the resistance to flow is dominated by the size and shape of the free space between the particles. In such situations, the particles are in physical contact with adjoining particles and there is little relative movement between the particles. In processes such as the sedimentation of particles in a liquid, however, each particle is completely surrounded by fluid and is free to move relative to other particles. Only very simple cases are capable of a precise theoretical analysis and Stokes’ law, which gives the drag on an isolated spherical particle due to its motion relative to the surrounding fluid at very low velocities, is the most important theoretical relation in this area of study. Indeed very many empirical laws are based on the concept of defining correction factors to be applied to Stokes’ law.

PARTICLE CHARACTERISATION

Single particles

The simplest shape of a particle is the sphere in that, because of its symmetry, any question of orientation does not have to be considered, since the particle looks exactly

the same from whatever direction it is viewed and behaves in the same manner in a fluid, irrespective of its orientation. No other particle has this characteristic. Frequently, the size of a particle of irregular shape is defined in terms of the size of an equivalent sphere although the particle is represented by a sphere of different size according to the property selected. Some of the important sizes of equivalent spheres are:

A. The sphere of the same volume as the particle.

B. The sphere of the same surface area as the particle.

C. The sphere of the same surface area per unit volume as the particle.

D. The sphere of the same area as the particle when projected on to a plane perpendicular to its direction of motion.

E. The sphere of the same projected area as the particle, as viewed from above, when lying in its position of maximum stability such as on a microscope slide for example.

F. The sphere which will just pass through the same size of square aperture as the particle, such as on a screen for example.

G. The sphere with the same settling velocity as the particle in a specified fluid.

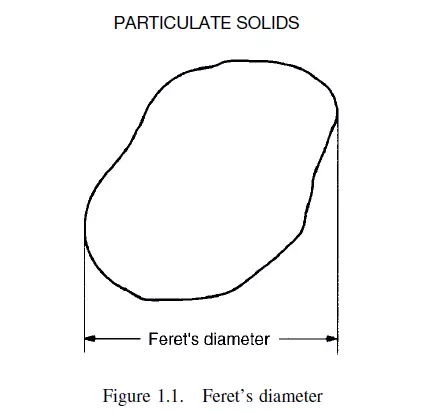
Several definitions depend on the measurement of a particle in a particular orientation. Thus Feret’s statistical diameter is the mean distance apart of two parallel lines which are tangential to the particle in an arbitrarily fixed direction, irrespective of the orientation of each particle coming up for inspection. This is shown in Figure 1.1.

A measure of particle shape which is frequently used is the sphericity, ψ, defined as:

Another method of indicating shape is to use the factor by which the cube of the size of the particle must be multiplied to give the volume. In this case the particle size is usually defined by method (e). Other properties of the particle which may be of importance are whether it is crystalline or amorphous, whether it is porous, and the properties of its surface, including roughness and presence of adsorbed films.

Hardness may also be important if the particle is subjected to heavy loading.

Measurement of particle size

Measurement of particle size and of particle size distribution is a highly specialised topic, and considerable skill is needed in the making of accurate measurements and in their interpretation. For details of the experimental techniques, reference should be made to a specialised text, and that of ALLEN(1) is highly recommended.

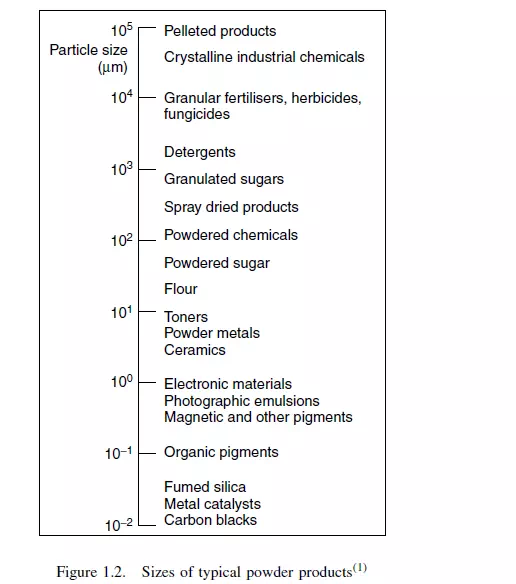
No attempt is made to give a detailed account or critical assessment of the various methods of measuring particle size, which may be seen from Figure 1.2 to cover a range

of 107 in linear dimension, or 1021 in volume! Only a brief account is given of some of the principal methods of measurement and, for further details, it is necessary to refer

to one of the specialist texts on particle size measurement, the outstanding example of which is the two-volume monograph by ALLEN(1), with HERDAN(2) providing additional information. It may be noted that both the size range in the sample and the particle shape may be as important, or even more so, than a single characteristic linear dimension which at best can represent only one single property of an individual particle or of an assembly of particles. The ability to make accurate and reliable measurements of particle size is acquired only after many years of practical experimental experience. For a comprehensive review of methods and experimental details it is recommended that the work of Allen be consulted and also Wardle’s work on Instrumentation and Control discussed in Volume 3. Before a size analysis can be carried out, it is necessary to collect a representative sample of the solids, and then to reduce this to the quantity which is required for the chosen method of analysis. Again, the work of Allen gives information on how this is best carried out. Samples will generally need to be taken from the bulk of the powder, whether this is in a static heap, in the form of an airborne dust, in a flowing or falling stream, or on a conveyor belt, and in each case the precautions which need to be takento obtain a representative sample are different.

 A wide range of measuring techniques is available both for single particles and for systems of particles. In practice, each method is applicable to a finite range of sizes and

gives a particular equivalent size, dependent on the nature of the method. The principles

of some of the chief methods are now considered together with an indication of the size range to which they are applicable.

Sieving (>50 μm)

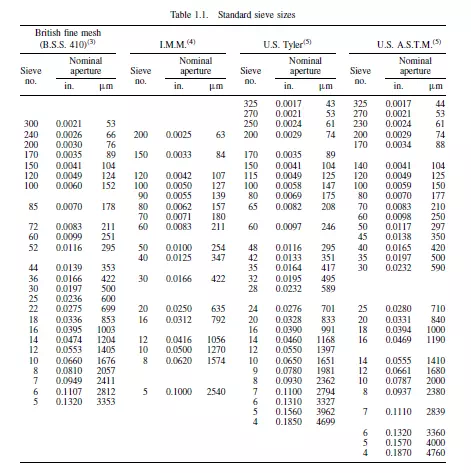
Sieve analysis may be carried out using a nest of sieves, each lower sieve being of smaller aperture size. Generally, sieve series are arranged so that the ratio of aperture

sizes on consecutive sieves is 2, 21/2 or 21/4 according to the closeness of sizing that is required. The sieves may either be mounted on a vibrator, which should be designed to give a degree of vertical movement in addition to the horizontal vibration, or may be hand shaken. Whether or not a particle passes through an aperture depends not only upon its size, but also on the probability that it will be presented at the required orientation at the surface of the screen. The sizing is based purely on the linear dimensions of the  particle and the lower limit of size which can be used is determined by two principal factors. The first is that the proportion of free space on the screen surface becomes very small as the size of the aperture is reduced. The second is that attractive forces between particles become larger at small particle sizes, and consequently particles tend to stick together and block the screen. Sieves are available in a number of standard series. There are several standard series of screen and the sizes of the openings are determined by the thickness of wire used. In the U.K., British Standard (B.S.)(3) screens are made in sizes from 300-mesh upwards, although these are too fragile for some work. The Institute of Mining and Metallurgy (I.M.M.)(4) screens are more robust, with the thickness of the wire approximately equal to the size of the apertures. The Tyler series, which is standard in the United States, is intermediate between the two British series. Details of the three series of screens(3) are given in Table 1.1, together with the American Society for Testing Materials (ASTM) series(5).

The efficiency of screening is defined as the ratio of the mass of material which passes the screen to that which is capable of passing. This will differ according to the size of the material. It may be assumed that the rate of passage of particles of a given size through the screen is proportional to the number or mass of particles of that size on the screen at any instant. Thus, if w is the mass of particles of a particular size on the screen at a time t , then:

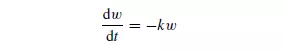
where k is a constant for a given size and shape of particle and for a given screen. Thus, the mass of particles (w1 − w2) passing the screen in time t is given by:

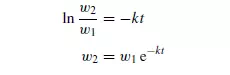
If the screen contains a large proportion of material just a little larger than the maximum size of particle which will pass, its capacity is considerably reduced. Screening is generally continued either for a predetermined time or until the rate of screening falls off to a certain fixed value. Screening may be carried out with either wet or dry material. In wet screening, material is washed evenly over the screen and clogging is prevented. In addition, small particles are washed off the surface of large ones. This has the obvious disadvantage, however, that it may be necessary to dry the material afterwards. With dry screening, the material is sometimes brushed lightly over the screen so as to form a thin even sheet. It is important that any agitation is not so vigorous that size reduction occurs, because screens are usually quite fragile and easily damaged by rough treatment. In general, the larger and the more abrasive the solids the more robust is the screen required.

Microscopic analysis (1–100 μm)

Microscopic examination permits measurement of the projected area of the particle and also enables an assessment to be made of its two-dimensional shape. In general, the

third dimension cannot be determined except when using special stereomicroscopes. The apparent size of particle is compared with that of circles engraved on a graticule in the eyepiece as shown in Figure 1.3. Automatic methods of scanning have been developed. By using the electron microscope(7), the lower limit of size can be reduced to about μm.

0

Sedimentation and elutriation methods (>1 μm)

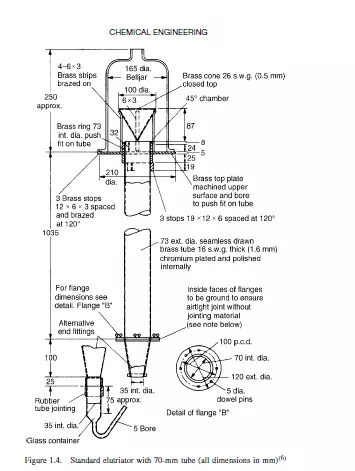
These methods depend on the fact that the terminal falling velocity of a particle in a fluid increases with size. Sedimentation methods are of two main types. In the first, the pipette method, samples are abstracted from the settling suspension at a fixed horizontal level at intervals of time. Each sample contains a representative sample of the suspension, with the exception of particles larger than a critical size, all of which will have settled below the level of the sampling point. The most commonly used equipment, the And reason pipette, is described by ALLEN(1). In the second method, which involves the use of the sedimentation balance, particles settle on an immersed balance pan which is  continuously weighed. The largest particles are deposited preferentially and consequently the rate of increase of weight falls off progressively as particles settle out. Sedimentation analyses must be carried out at concentrations which are sufficiently low for interactive effects between particles to be negligible so that their terminal falling velocities can be taken as equal to those of isolated particles. Careful temperature control (preferably to ±0.1 deg K) is necessary to suppress convection currents. The lower limit of particle size is set by the increasing importance of Brownian motion for progressively smaller particles. It is possible however, to replace gravitational forces by centrifugal forces and this reduces the lower size limit to about 0.05 μm.  The elutriation method is really a reverse sedimentation process in which the particles are dispersed in an upward flowing stream of fluid. All particles with terminal falling velocities less than the upward velocity of the fluid will be carried away. A complete size analysis can be obtained by using successively higher fluid velocities. Figure 1.4 shows the standard elutriator (BS 893)(6) for particles with settling velocities between 7 and 70 mm/s.

Permeability methods (>1 μm)

These methods depend on the fact that at low flowrates the flow through a packed bed is directly proportional to the pressure difference, the proportionality constant being proportional to the square of the specific surface (surface : volume ratio) of the powder. From this method it is possible to obtain the diameter of the sphere with the same specific surface as the powder. The reliability of the method is dependent upon the care with which the sample of powder is packed. Further details are given in Chapter 4.

Electronic particle counters

A suspension of particles in an electrolyte is drawn through a small orifice on either side of which is positioned an electrode. A constant electrical current supply is connected to the electrodes and the electrolyte within the orifice constitutes the main resistive component of the circuit. As particles enter the orifice they displace an equivalent volume of electrolyte, thereby producing a change in the electrical resistance of the circuit, the magnitude of which is related to the displaced volume. The consequent voltage pulse  across the electrodes is fed to a multi-channel analyser. The distribution of pulses arising from the passage of many thousands of particles is then processed to provide a particle (volume) size distribution.  The main disadvantage of the method is that the suspension medium must be so highly conducting that its ionic strength may be such that surface active additives may be

required in order to maintain colloidal stability of fine particle suspensions as discussed in Section 5.2.2. The technique is suitable for the analysis of non-conducting particles and for conducting particles when electrical double layers confer a suitable degree of electrical insulation. This is also discussed in Section 5.2.2.  By using orifices of various diameters, different particle size ranges may be examined and the resulting data may then be combined to provide size distributions extending over a large proportion of the sub-millimetre size range. The prior removal from the suspension of particles of sizes upwards of about 60 per cent of the orifice diameter helps to prevent

problems associated with blocking of the orifice. The Coulter Counter and the Elzone Analyser work on this principle.

Laser diffraction analysers

These instruments(8) exploit the radial light scattering distribution functions of particles. A suspension of particles is held in, or more usually passed across, the path of a collimated beam of laser light, and the radially scattered light is collected by an array of photodetectors positioned perpendicular to the optical axis. The scattered light distribution is sampled and processed using appropriate scattering models to provide a particle size distribution. The method is applicable to the analysis of a range of different particles in a variety of media. Consequently, it is possible to examine aggregation phenomenas as discussed in Section 5.4, and to monitor particle size for on-line control of process streams. Instruments are available which provide particle size information over the range 0.1–600 μm. Light scattered from particles smaller than 1 μm is strongly influenced by their optical properties and care is required in data processing and interpretation.  The scattering models employed in data processing invariably involve the assumption of particle sphericity. Size data obtained from the analysis of suspensions of asymmetrical particles using laser diffraction tend to be somewhat more ambiguous than those obtained by electronic particle counting, where the solid volumes of the particles are detected.

X-ray or photo-sedimentometers

Information on particle size may be obtained from the sedimentation of particles in dilute suspensions. The use of pipette techniques can be rather tedious and care is required to ensure that measurements are sufficiently precise. Instruments such as X-ray or photo sedimentometers serve to automate this method in a non-intrusive manner. The attenuation of a narrow collimated beam of radiation passing horizontally through a sample of suspension is related to the mass of solid material in the path of the beam. This attenuation can be monitored at a fixed height in the suspension, or can be monitored as the beam is raised at a known rate. This latter procedure serves to reduce the time required to obtain sufficient data from which the particle size distribution may be calculated. This technique is limited to the analysis of particles whose settling behaviour follows Stokes’ law, as discussed in Section 3.3.4, and to conditions where any diffusive motion of particles is negligible.

Sub-micron particle sizing

Particles of a size of less than 2 μm are of particular interest in Process Engineering because of their large specific surface and colloidal properties, as discussed in Section 5.2. The diffusive velocities of such particles are significant in comparison with their settling velocities. Provided that the particles scatter light, dynamic light scattering techniques, such as photon correlation spectroscopy (PCS), may be used to provide information about particle diffusion.  In the PCS technique, a quiescent particle suspension behaves as an array of mobile scattering centres over which the coherence of an incident laser light beam is preserved. The frequency of the light intensity fluctuations at a point outside the incident light path is related to the time taken for a particle to diffuse a distance equivalent to the wavelength of the incident light. The dynamic light signal at such a point is sampled and correlated with itself at different time intervals using a digital correlator and associated computer software. The relationship of the (so-called) auto-correlation function to the time intervals is processed to provide estimates of an average particle size and variance (polydispersity index). Analysis of the signals at different scattering angles enables more detailed information to be obtained about the size distribution of this fine, and usually

problematical, end of the size spectrum. The technique allows fine particles to be examined in a liquid environment so that estimates can be made of their effective hydrodynamic sizes. This is not possible using other techniques.

Provided that fluid motion is uniform in the illuminated region of the suspension, then similar information may also be extracted by analysis of laser light scattering from

particles undergoing electrophoretic motion, that is migratory motion in an electric field, superimposed on that motion. Instrumentation and data processing techniques for systems employing dynamic light scattering for the examination of fine particle motion are currently under development.