What is Molecular Orbital Theory?
The Molecular Orbital Theory (often abbreviated to MOT) is a theory on chemical bonding developed at the beginning of the twentieth century by F. Hund and R. S. Mulliken to describe the structure and properties of different molecules. The valence-bond theory failed to adequately explain how certain molecules contain two or more equivalent bonds whose bond orders lie between that of a single bond and that of a double bond, such as the bonds in resonance-stabilized molecules. This is where the molecular orbital theory proved to be more powerful than the valence-bond theory (since the orbitals described by the MOT reflect the geometries of the molecules to which it is applied).
The key features of the molecular orbital theory are listed below.
In simple terms, the molecular orbital theory states that each atom tends to combine together and form molecular orbitals. As a result of such arrangement, electrons are found in various atomic orbitals and they are usually associated with different nuclei. In short, an electron in a molecule can be present anywhere in the molecule.
One of the main impacts of the molecular orbital theory after its formulation is that it paved a new way to understand the process of bonding. With this theory, the molecular orbitals are basically considered as linear combinations of atomic orbitals. The approximations are further done using the Hartree–Fock (HF) or the density functional theory (DFT) models to the Schrödinger equation.
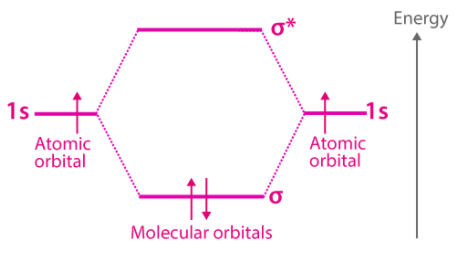
Molecular orbital theory approximation of the molecular orbitals as linear combinations of atomic orbitals can be illustrated as follows.

However, to understand the molecular orbital theory more clearly and in-depth, it is important to understand what atomic and molecular orbitals are first?
Linear Combination of Atomic Orbitals (LCAO)
Molecular orbitals can generally be expressed through a linear combination of atomic orbitals (abbreviated to LCAO). These LCAOs are useful in the estimation of the formation of these orbitals in the bonding between the atoms that make up a molecule.
The Schrodinger equation used to describe the electron behaviour for molecular orbitals can be written in a method similar to that for atomic orbitals.
It is an approximate method for representing molecular orbitals. It’s more of a superimposition method where constructive interference of two atomic wave function produces a bonding molecular orbital whereas destructive interference produces non-bonding molecular orbital.
The conditions that are required for the linear combination of atomic orbitals are as follows:
The atomic orbitals combining to form molecular orbitals should have comparable energy. This means that 2p orbital of an atom can combine with another 2p orbital of another atom but 1s and 2p cannot combine together as they have appreciable energy difference.
The combining atoms should have the same symmetry around the molecular axis for proper combination, otherwise, the electron density will be sparse. For e.g. all the sub-orbitals of 2p have the same energy but still, 2pz orbital of an atom can only combine with a 2pz orbital of another atom but cannot combine with 2px and 2py orbital as they have a different axis of symmetry. In general, the z-axis is considered as the molecular axis of symmetry.
The two atomic orbitals will combine to form molecular orbital if the overlap is proper. Greater the extent of overlap of orbitals, greater will be the nuclear density between the nuclei of the two atoms.
The condition can be understood by two simple requirements. For the formation of proper molecular orbital, proper energy and orientation are required. For proper energy, the two atomic orbitals should have the same energy and for the proper orientation, the atomic orbitals should have proper overlap and the same molecular axis of symmetry.