Longest common subsequence problem

You’ll first see how to use dynamic programming to find a longest common subsequence (LCS) of two DNA sequences. Biologists who find a new gene sequence typically want to know what other sequences it is most similar to. Finding an LCS is one way of computing how similar two sequences are: the longer the LCS is, the more similar they are.

The characters in a subsequence, unlike those in a substring, do not need to be contiguous. For example, ACE is a subsequence (but not a substring) of ABCDE. Consider the following two DNA sequences:

• S1 = GCCCTAGCG
• S2 = GCGCAATG

It turns out that an LCS of these two sequences is GCCAG. (Note that this is an LCS, rather than the LCS, because other common subsequences of the same length might exist. This and the other optimization problems you’ll look at might have more than one solution.)

LCS algorithm

First, think about how you might compute an LCS recursively. Let:

• C1 be the right-most character of S1
• C2 be the right-most character of S2
• S1′ be S1 with C1 “chopped-off”
• S2′ be S2 with C2 “chopped-off”

There are three recursive subproblems:

• L1 = LCS(S1′, S2)
• L2 = LCS(S1, S2′)
• L3 = LCS(S1′, S2′)

I won’t prove this, but it can be shown (and it’s not hard to believe) that the solution to the original problem is whichever of these is the longest:

• L1
• L2
• L3 appended with C1 if C1 equals C2, or L3 if C1 is not equal to C2

(The base case is whenever S1 or S2 is a zero-length string. In this case, the LCS of S1 and S2 is clearly a zero-length string.)

However, like the recursive procedure for computing Fibonacci numbers, this recursive solution requires multiple computations of the same subproblems. It can be shown that this recursive solution takes exponential time to run. In contrast, the dynamic programming solution to this problem runs in Θ(mn) time, where m and n are the lengths of the two sequences.

To compute the LCS efficiently using dynamic programming, you start by constructing a table in which you build up partial results. List one of the sequences across the top and the other down the left, as shown in Figure 2:

Figure 2. Initial LCS table

The idea is that you’ll fill up the table from top to bottom, and from left to right, and each cell will contain a number that is the length of an LCS of the two string prefixes up to that row and column. That is, each cell will contain a solution to a subproblem of the original problem. For example, consider the cell in the sixth row and the seventh column; it is to the right of the second C in GCGCAATG and below the T in GCCCTAGCG. This cell will eventually contain a number that is the length of an LCS of GCGC and GCCCT.

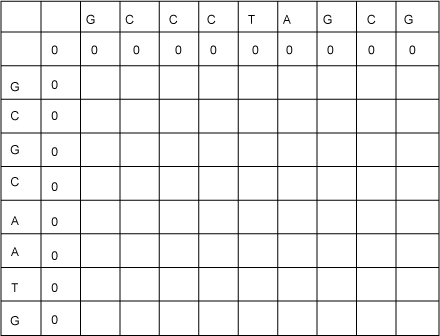
First consider what the entries should be for the table’s second row. These are the lengths of LCSs for the zero-length prefix of the sequence going down the left, GCGCAATG, and prefixes of the sequence along the top, GCCCTAGCG. Clearly, the value of any of these LCSs will be 0. Similarly, the values down the second columns will all be 0. This corresponds to the base case of the recursive solution. Now the table looks like Figure 3:

Figure 3. LCS table with base cases filled in

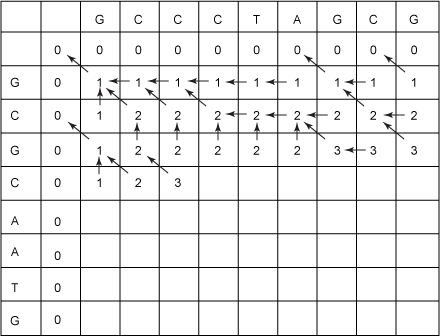
Next, you implement what corresponds to the recursive subcases in the recursive algorithm, but you use values that you’ve already filled in. In Figure 4, I’ve filled in about half of the cells:

Figure 4. LCS table half filled-in

When you fill in a cell, you consider:

• The cell directly to the left of it
• The cell directly above it
• The cell to the above-left of it

The three values below correspond, respectively, to the values returned by the three recursive subproblems I listed earlier.

• V1 = the value in the cell to the left
• V2 = the value in the cell above
• V3 = the value in the cell to the above-left

You fill in the empty cell with the maximum of these three numbers:

• V1
• V2
• V3 + 1 if C1 equals C2, or V3 if C1 is not equal to C2, where C1 is the character above the current cell and C2 is the character to the left of the current cell

Note that I also add arrows that point back to which of those three cells I used to get the value for the current cell. You’ll use these arrows later in “tracing back” to construct an actual LCS (as opposed to just discovering the length of one).

Now fill in the next blank cell in Figure 4 — the one under the third C in GCCCTAGCG and to the right of the second C in GCGCAATG. You have a 2 above it, a 3 to the left of it, and a 2 to the above-left of it. The character above this cell and the character to the left of this cell are equal (they’re both C), so you must pick the maximum of 2, 3, and 3 (2 from the above-left cell + 1). So, the value of this cell will be 3. Draw an arrow back to the cell from which you got this new number. In this case, where the new number could have come from more than one cell, pick an arbitrary one: the one to the above-left, say.

As an exercise, you might want to try filling in the rest of the table. If, in the case of ties, you always choose the cell to the above-left over the cell above and the cell above over the cell to the left, you’ll get the table in Figure 5. (If you make different choices in the case of ties, your arrows will be different, of course, but the numbers will be the same.)

Figure 5. Filled-in LCS table

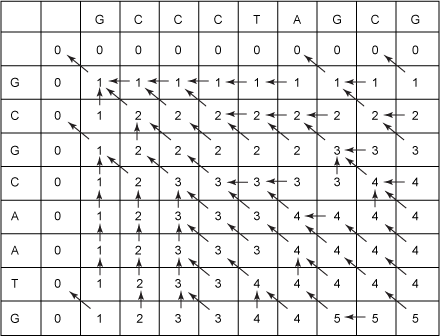
Recall that the number in any cell is the length of an LCS of the string prefixes above and below that end in the column and row of that cell. Hence, the number in the lower, right-most cell is the length of an LCS of the two strings S1 and S2— GCCCTAGCG and GCGCAATG in this case. So, the length of an LCS for these two sequences is 5.