Condensing one tree into another

Okay, so now we have two trees to keep straight in our heads. We already had a parse tree, and how there’s yet another data structure to learn! And apparently, this AST data structure is just a simplified parse tree. So, why do we need it? What even is the point of it?

Well, let’s take a look at our parse tree, shall we?

We already know that parse trees represent our program at its most distinct parts; indeed, this was why the scanner and the tokenizer have such important jobs of breaking down our expression into its smallest parts!

What does it mean to actually represent a program by its most distinct parts?

As it turns out, sometimes all of the distinct parts of a program actually aren’t all that useful to us all the time.

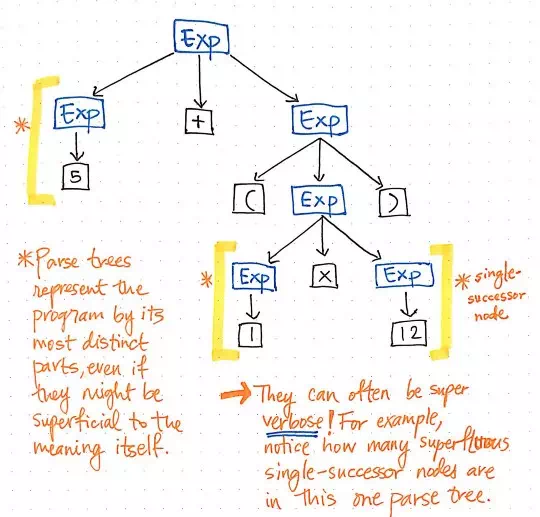
Parse tree can often be super verbose.

Let’s take a look at the illustration shown here, which represents our original expression, 5 + (1 x 12), in parse tree tree format. If we take a close look at this tree with a critical eye, we’ll see that there are a few instances where one node has exactly one child, which are also referred to as single-successor nodes, as they only have one child node stemming from them (or one “successor”).

In the case of our parse tree example, the single-successor nodes have a parent node of an Expression, or Exp, which have a single successor of some value, such as 5, 1, or 12. However, the Exp parent nodes here aren’t actually adding anything of value to us, are they? We can see that they contain token/terminal child nodes, but we don’t really care about the “expression” parent node; all we really want to know is what is the expression?

The parent node doesn’t give us any additional information at all once we’ve parsed our tree. Instead, what we’re really concerned with is the single child, single-successor node. Indeed, that is the node that gives us the important information, the part that is significant to us: the number and value itself! Considering the fact that these parent nodes are kind of unnecessary to us, it becomes obvious that this parse tree is a kind of verbose.

All of these single-successor nodes are pretty superfluous to us, and don’t help us at all. So, let’s get rid of them!

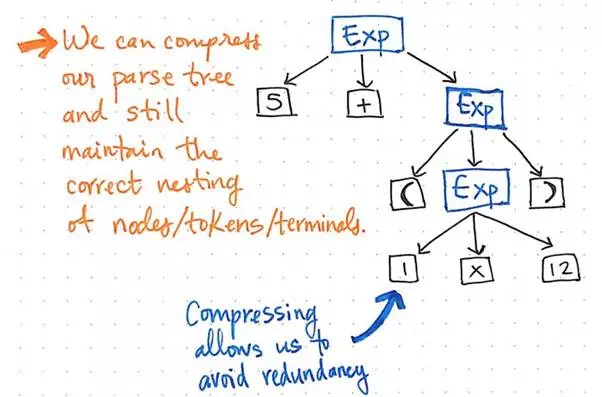
Compressing a parse tree allows us to avoid redundancy.

If we compress the single-successor nodes in our parse tree, we’ll end up with a more compressed version of the same exact structure. Looking at the illustration above, we’ll see that we’re still maintaining the exact same nesting as before, and our nodes/tokens/terminals are still appearing in the correct place within the tree. But, we’ve managed to slim it down a bit.

And we can trim some more of our tree, too. For example, if we look at our parse tree as it stands at the moment, we’ll see that there’s a mirror structure within it. The sub-expression of (1 x 12) is nested within parentheses (), which are tokens by their own right.

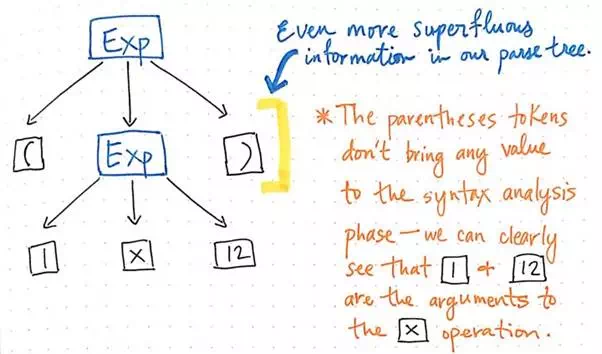
Superfluous information that is of no use to us can be removed from a parse tree.

However, these parentheses don’t really help us once we’ve got our tree in place. We already know that 1 and 12 are arguments that will be passed to the multiplication x operation, so the parentheses don’t tell us all that much at this point. In fact, we could compress our parse tree even further and get rid of these superfluous leaf nodes.

Once we compress and simplify our parse tree and get rid of the extraneous syntactic “dust”, we end up with a structure that looks visibly different at this point. That structure is, in fact, our new and much-anticipated friend: the abstract syntax tree.

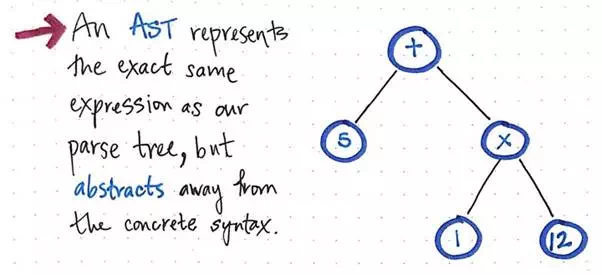
An AST abstracts away from the concrete syntax.

The image above illustrates the exact same expression as our parse tree: 5 + (1 x 12). The difference is that it has abstracted away the expression from the concrete syntax. We don’t see any more of the parentheses () in this tree, because they’re not necessary. Similarly, we don’t see non-terminals like Exp, since we’ve already figured out what the “expression” is, and we are able to pull out the value that really matters to us — for example, the number 5.

This is exactly the distinguishing factor between an AST and a CST. We know that an abstract syntax tree ignores a significant amount of the syntactic information that a parse tree contains, and skips “extra content” that is used in parsing. But now we can see exactly how that happens!

An AST is an abstract representation of a source text.

Now that we’ve condensed a parse tree of our own, we’ll be much better at picking up on some of the patterns that distinguish an AST from a CST.

There a few ways that an abstract syntax tree will visually-differ from a parse tree:

1. An AST will never contain syntactic details, such as commas, parentheses, and semicolons (depending, of course, upon the language).

2. An AST will have collapsed version of what would otherwise appear as single-successor nodes; it will never contain “chains” of nodes with a single child.

3. Finally, any operator tokens (such as +, -, x, and /) will become internal (parent) nodes in the tree, rather than the leaves which terminate in a parse tree.

Visually, an AST will always appear more compact than a parse tree, since it is, by definition, a compressed version of a parse tree, with less syntactic detail.

It would stand to reason, then, that if an AST is a compacted version of a parse tree, we can only really create an abstract syntax tree if we have the things to build a parse tree to begin with!

This is, indeed, how the abstract syntax tree fits into the larger compilation process. An AST has a direct connection to the parse trees that we have already learned about, while simultaneously relying upon the lexer to do its job before an AST can ever be created.

An AST is always the output of the parser.

The abstract syntax tree is created as the final result of the syntax analysis phase. The parser, which is front and center as the main “character” during syntax analysis, may or may not always generate a parse tree, or CST. Depending on the compiler itself, and how it was designed, the parser may directly go straight onto constructing a syntax tree, or AST. But the parser will always generate an AST as its output, no matter whether it creates a parse tree in between, or how many passes it might need to take in order to do so.