BOTTOM-UP PARSING

Constructing a parse tree for an input string beginning at the leaves and going towards the root is called bottom-up parsing. A general type of bottom-up parser is a shift-reduce parser.

SHIFT-REDUCE PARSING

Shift-reduce parsing is a type of bottom-up parsing that attempts to construct a parse tree for an input string beginning at the leaves (the bottom) and working up towards the root (the top).

Example:

Consider the grammar:

S → aABe

A → Abc | b

B → d

The sentence to be recognized is abbcde.

REDUCTION (LEFTMOST) RIGHTMOST DERIVATION

abbcde (A → b) S → aABe

aAbcde(A → Abc) → aAde

aAde (B → d) → aAbcde

aABe (S → aABe) → abbcde

The reductions trace out the right-most derivation in reverse.

Handles:

A handle of a string is a substring that matches the right side of a production, and whose reduction to the non-terminal on the left side of the production represents one step along the reverse of a rightmost derivation.

Example:

Consider the grammar:

E→E+E

E→E*E

E→(E)

E→id

And the input string id1+id2*id3

The rightmost derivation is :

E→E+E

→ E+E*E

→ E+E*id3

→ E+id2*id3

→ id1+id2*

In the above derivation the underlined substrings are called handles.

Handle pruning:

A rightmost derivation in reverse can be obtained by “handle pruning”. (i.e.) if w is a sentence or string of the grammar at hand, then w = γn, where γn is the nth rightsentinel form of

some rightmost derivation.

Actions in shift-reduce parser:

• shift - The next input symbol is shifted onto the top of the stack.

• reduce - The parser replaces the handle within a stack with a non-terminal.

• accept - The parser announces successful completion of parsing.

• error - The parser discovers that a syntax error has occurred and calls an error recovery routine.

Conflicts in shift-reduce parsing:

There are two conflicts that occur in shift-reduce parsing:

1. Shift-reduce conflict: The parser cannot decide whether to shift or to reduce.

2. Reduce-reduce conflict: The parser cannot decide which of several reductions to make.

Stack implementation of shift-reduce parsing :

1. Shift-reduce conflict:

Example:

Consider the grammar:

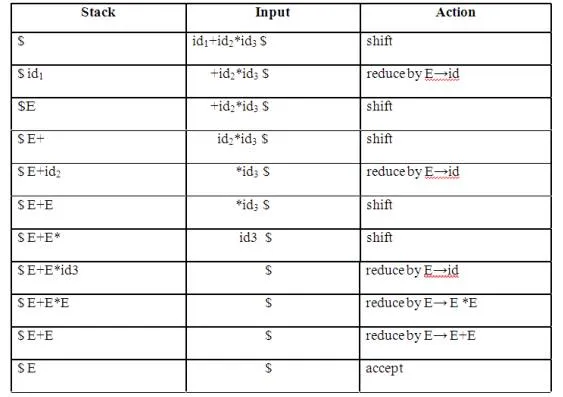
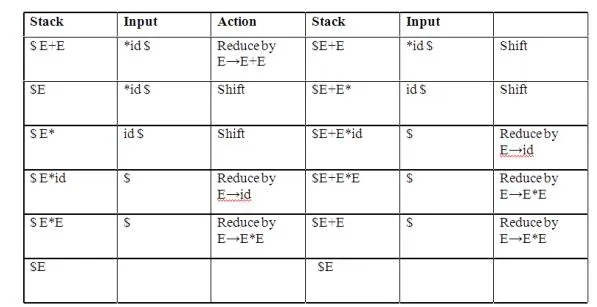
E→E+E | E*E | id and input id+id*id

2. Reduce-reduce conflict:

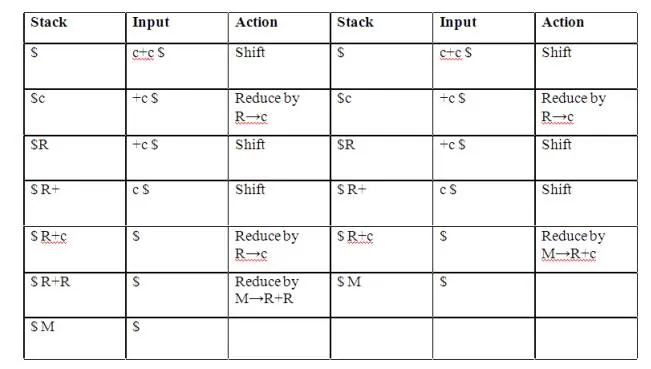
Consider the grammar: M→R+R|R+c|R

R→c

and input c+c

Viable prefixes:

α is a viable prefix of the grammar if there is w such that αw is a right

The set of prefixes of right sentinel forms that can appear on the stack of a shift-reduce parser are called viable prefixes

The set of viable prefixes is a regular language.

OPERATOR-PRECEDENCE PARSING

An efficient way of constructing shift-reduce parser is called operator-precedence parsing. Operator precedence parser can be constructed from a grammar called Operator-grammar. These grammars have the property that no production on right side is ɛor has two adjacent non-terminals.

Example:

Consider the grammar:

E→EAE|(E)|-E|id

A→+|-|*|/|↑

Since the right side EAE has three consecutive non-terminals, the grammar can be written as follows: E→E+E|E-E|E*E|E/E|E↑E |-E|id

Operator precedence relations:

There are three disjoint precedence relations namely

<. - less than

= - equal to

.> - greater than

The relations give the following meaning:

a<.b - a yields precedence to b

a=b - a has the same precedence as b

a.>b - a takes precedence over b

Rules for binary operations:

1. If operator θ1 has higher precedence than operator θ2, then make

θ1 . > θ2 and θ2 < . θ1

2. If operators θ1 and θ2, are of equal precedence, then make

θ1 . > θ2 and θ2 . > θ1 if operators are left associative

θ1 < . θ2 and θ2 < . θ1 if right associative

3. Make the following for all operators θ:

θ <. id ,id.>θ

θ <.(, (<.θ

).>θ, θ.>)

θ.>$ , $<. θ

Also make

( = ) , ( <. ( , ) .> ) , (<. id, id .>) , $ <. id , id .> $ , $ Example:

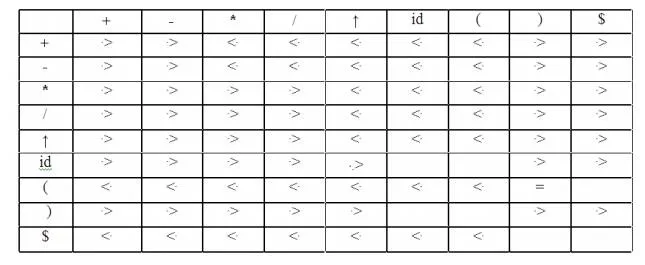
Operator-precedence relations for the grammar

E→E+E|E-E|E*E|E/E|E↑E |(E)|-E|idis given in the following table assuming

1. ↑ is of highest precedence and right-associative

2. * and / are of next higher precedence and left-associative, and

3. + and - are of lowest precedence and left- Note that the blanks in the table denote error entries.

Table : Operator-precedence relations

Operator precedence parsing algorithm:

Input : An input string w and a table of precedence relations.

Output : If w is well formed, a skeletal parse tree ,with a placeholder non-terminal E labeling all interior nodes; otherwise, an error indication.

Method : Initially the stack contains $ and the input buffer the string w $. To parse, we execute the following program :

(1) Set ip to point to the first symbol of w$;

(2) repeat forever

(3) if $ is on top of the stack and ip points to $ then

(4) return else begin

(5) let a be the topmost terminal symbol on the stack and let b be the symbol pointed to by ip;

(6) if a <. b or a = b then begin

(7) push b onto the stack;

(8) advance ip to the next input symbol; end;

(9) else if a . > b then /*reduce*/

(10) repeat

(11) pop the stack

(12) until the top stack terminal is related by <.to the terminal most recently popped

(13) else error( ) end

Stack implementation of operator precedence parsing:

Operator precedence parsing uses a stack and precedence relation table for its implementation of above algorithm. It is a shift-reduce parsing containing all four actions shift, reduce, accept and error.

The initial configuration of an operator precedence parsing is

STACK : $

INPUT : w$

where w is the input string to be parsed.

Example:

Consider the grammar E → E+E | E-E | E*E | E/E | E↑E | (E) | id. Input string is id+id*id .The implementation is as follows:

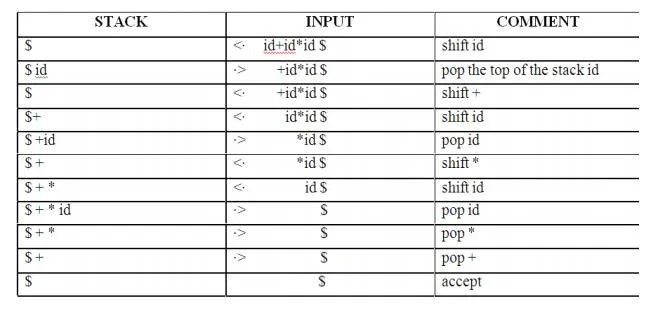
Advantages of operator precedence parsing:

1. It is easy to implement.

2. Once an operator precedence relation is made between all pairs of terminals of a grammar, the grammar can be ignored. The grammar is not referred anymore during implementation.

Disadvantages of operator precedence parsing:

1. It is hard to handle tokens like the minus sign (-) which has two different precedence.

2. Only a small class of grammar can be parsed using operator-precedence parser.