Game Playing
Game Playing is an important domain of artificial intelligence. Games don’t require much knowledge; the only knowledge we need to provide is the rules, legal moves and the conditions of winning or losing the game.
Both players try to win the game. So, both of them try to make the best move possible at each turn. Searching techniques like BFS(Breadth First Search) are not accurate for this as the branching factor is very high, so searching will take a lot of time. So, we need another search procedures that improve –
· Generate procedure so that only good moves are generated.
· Test procedure so that the best move can be explored first.
The most common search technique in game playing is Minimax search procedure. It is depth-first depth-limited search procedure. It is used for games like chess and tic-tac-toe.
Minimax algorithm uses two functions –
MOVEGEN : It generates all the possible moves that can be generated from the current position.
STATICEVALUATION : It returns a value depending upon the goodness from the viewpoint otwo-player
This algorithm is a two player game, so we call the first player as PLAYER1 and second player as PLAYER2. The value of each node is backed-up from its children. For PLAYER1 the backed-up value is the maximum value of its children and for PLAYER2 the backed-up value is the minimum value of its children. It provides most promising move to PLAYER1, assuming that the PLAYER2 has make the best move. It is a recursive algorithm, as same procedure occurs at each level.

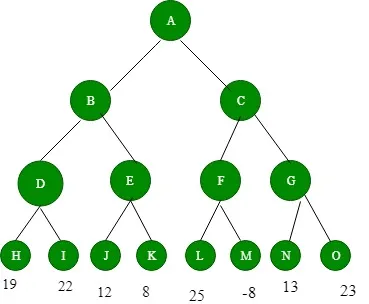
Figure 1: Before backing-up of values
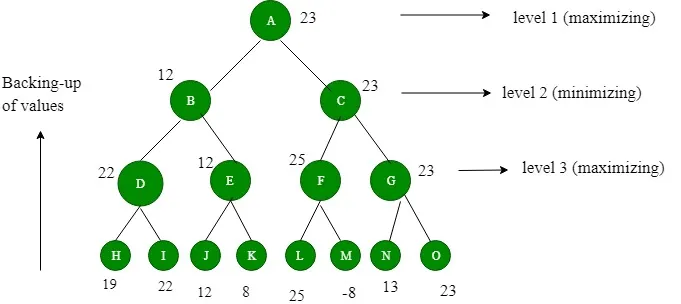
Figure 2: After backing-up of values
We assume that PLAYER1 will start the game. 4 levels are generated. The value to nodes H, I, J, K, L, M, N, O is provided by STATICEVALUATION function. Level 3 is maximizing level, so all nodes of level 3 will take maximum values of their children. Level 2 is minimizing level, so all its nodes will take minimum values of their children. This process continues. The value of A is 23. That means A should choose C move to win.