Reasoning Systems for Categories

2 families of systems designed for organizing and reasoning with categories:

§  semantic networks - utilizing graphs and algorithms for inferring properties of an object on the basis of its category membership

§  description logics - provides a formal language for constructing and combining category definitions and algorithms for deciding subset and superset relationships between categories

Semantic Networks

A typical graphical notation displays object or category names in ovals or boxes, and connects them with labeled links. For example, Figure 12.5 has a MemberOf link between Mary and FemalePersons, corresponding to the logical assertion Mary ∈ FemalePersons; similarly, the SisterOf link between Mary and John corresponds to the assertion SisterOf(Mary, John). We can connect categories using SubsetOf links, and so on. It is such fun drawing bubbles and arrows that one can get carried away. For example, we know that persons have female persons as mothers, so can we draw a HasMother link from Persons to FemalePersons? The answer is no, because HasMother is a relation between a person and his or her mother, and categories do not have mothers.

For this reason, we have used a special notation (the double-boxed link) in Figure 12.5. This link asserts that

We might also want to assert that persons have two legs (the singly-boxed link) in Figure 12.5

As before, we need to be careful not to assert that a category has legs; the single-boxed link in Figure 12.5 is used to assert properties of every member of a category.

semantic network notation makes it convenient to perform inheritance reasoning. However, inheritance becomes complicated when an object can belong to more than one category or when a category can be a subset of more than one other category; this is called multiple inheritance

Semantic Networks - Default Values

semantic network also has the ability to represent default values for categories. we say the default value is overridden by the more specific value (e.g. figure 12.5 John has 1 leg even though he is a person and all persons have 2 legs)

Drawbacks of Semantic Networks

§  one drawback of semantic network notation (compared to first-order logic) is that links between nodes/bubbles represent only binary relations. 
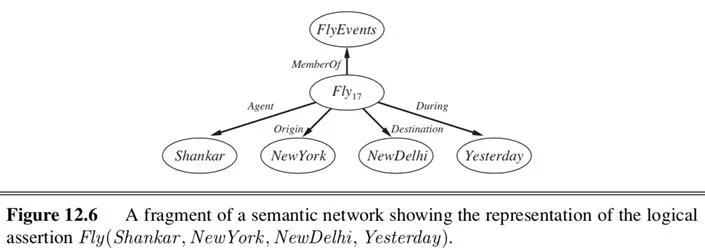
for example, to represent the following sentence in semantic networks is shown in figure 12.6 by reifying the proposition itself as an event belonging to an appropriate event category

§ 

§  another drawback for this simple version of semantic networks, is that it still leaves out the full first-order logic such as representing negation, disjunction, nested function symbols, and existential quantification.

Description Logics

syntax of first-order logic makes it easy to say things about objects

description logics

§  are notations that make it easier to describe definitions and properties of categories

§  evolved from semantic networks in response to pressure to formalizing what networks mean while retaining emphasis on taxonomic structure

§  the principle inference tasks of description logics are:

§  subsumption - checking if one category is a subset of another by comparing their definitions

§  classification - checking whether an object belongs to a category

§  consistency - some description logic system includes consistency of a category definition (whether the membership criteria are logically satisfiable)

the CLASSIC language (Borgida et al., 1989) is a typical description logic

syntax of CLASSIC descriptions shown in figure 12.7

for example, to say "bachelors are unmarried adult males":

the equivalent in first-order logic:

any description in CLASSIC description logic can be translated into an equivalent first-order logic sentence. but some are more straightforward in CLASSIC description logic. for example, to describe the set of men with at least 3 sons who are all unemployed and married to doctors, and at most 2 daughters who are all professors in physics or math departments:

Description Logic - Its Tractability and its Drawbacks

the most important aspect of description logics is their emphasis on tractability of inference.

a problem instance is solved by describing it and then asking if it is subsumed by one of several possible solution categories. In standard first-order logic systems, predicting the solution time is often impossible. It is frequently left to the user to engineer the representation to detour around sets of sentences that seem to be causing the system to take several weeks to solve a problem. Description logics, on the other hand, is to ensure that subsumption-testing can be solved in time polynomial in the size of the descriptions

this sounds wonderful in principle, until one realizes that it can only have one of 2 consequences:

§  either hard problems cannot be stated at all

§  or they require exponentially large descriptions

However, the tractability results do shed light on what sorts of constructs cause problems and thus help the user to understand how different representations behave. For example, description logics usually lack negation and disjunction. Each forces first- order logical systems to go through a potentially exponential case analysis in order to ensure completeness. CLASSIC allows only a limited form of disjunction in the Fills and OneOf constructs, which permit disjunction over explicitly enumerated individuals but not over descriptions. With disjunctive descriptions, nested definitions can lead easily to an exponential number of alternative routes by which one category can subsume another