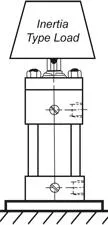
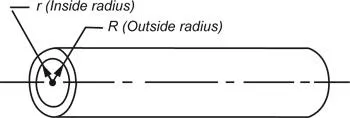
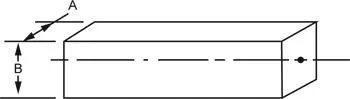
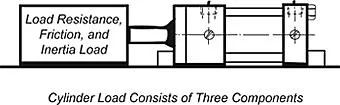
Force Required to Accelerate a Load

The load on a hydraulic cylinder (or motor) consists of these three components:

(1). Normal load resistance, where fluid power is converted into mechanical work exerted against the load.

(2). Friction resistance, where some of the fluid power is expended in overcoming friction.

(3). Inertia, where fluid power is needed to get a massive load into motion, sometimes very quickly.

As far as Items (1) and (2) are concerned, acceleration to final velocity would be instantaneous as soon as the fluid power is applied to the cylinder (or motor).

If the load has high inertia due to high mass, as in Item (3), then an additional amount of pressure must be supplied to accelerate the load from standstill to final velocity in a desired interval of time.

This power due to extra pressure is carried as kinetic energy while the load is moving at a constant velocity, and may come back into the system as shock and heat when the load is stopped, unless it can be absorbed by the load in the form of work.

The purpose of this data sheet is to show how to calculate the extra pressure or torque needed in a hydraulic system to accelerate an inertia load, Item (3), from standstill to its final velocity in a given time, assuming the pressure needed for Items (1) and (2), the work load and the friction resistance has already been calculated or assumed.

Calculating for Inertia Load ...

Before calculating the extra PSI needed to rapidly accelerate this vertically moving cylinder, the normal PSI needed to move the load at a constant speed must be calculated by the usual method: Load weight ÷ Piston Area. Allowance should also be made for friction in the ways or guides if significant.

Use the following formula to calculate the extra PSI for acceleration to a final velocity in a specified time:

(a). F = (V x W) ÷ (g x t) Lbs, in which:
F is the accelerating force, in lbs, that will be needed.
V is the final velocity, in feet per second, starting from standstill.
W is the load weight, in lbs.
g is acceleration of gravity to convert weight into mass, always 32.16
t is the time, in seconds, during which acceleration will take place.

If the cylinder bore is known, the accelerating force for its piston can be found directly from the formula:

(b). PSI = V x W ÷ (A x g x t), in which:
A is piston area in square inches. Other symbols are same as above.

 

Problem Data - Vertical Cylinder with Inertia Load

Steady Load= 35,000 lbs.
Cylinder Bore= 4" (Piston Area= 12.57 sq.ins.)

Initial Velocity= 0; Final Velocity= 12ft/sec.
Time Required to Accelerate= 2 Seconds

Example of Inertia Calculation... Use the problem data in the box to solve for the total PSI needed on the vertically moving cylinder not only to lift the given load, but to accelerate it to its final velocity in the specified time. Or to accelerate it from a lower to a higher velocity.

PSI for Steady Movement... 35,000 lbs. (load weight) ÷ 12.57 (piston area) = 2784 PSI needed to raise the load.

PSI for Acceleration... PSI = (12 x 35,000) ÷ (12.57 x 32.16 x 2) = 520 PSI.

Total PSI... The cylinder must be provided with 2784 + 520 = 3304 PSI to meet all conditions of the problem.

Non-Inertia Loads... No significant extra PSI is needed to accelerate work loads which consist almost entirely of frictional resistance and negligible mass.

Moment of Inertia of Rotating Load...
The moment of inertia, indicated with symbol J in the formula in the opposite column, must be calculated before accelerating torque can be figured. Examples for three common shapes are shown here. Many other shapes are shown in machinery handbooks.

HOLLOW CYLINDER (Pipe)...
J (moment of inertia) of a pipe about an axis running lengthwise is:
J = W x (R2 + r2) ÷ 2g lnch-Lbs-Secs2 , in which:
W is total weight of pipe in pounds
R is outside radius of pipe in inches
r is inside radius of pipe in inches
g is acceleration of gravity, always 32.16

SOLID CYLINDER...
J (moment of inertia) of a solid cylinder about an axis running lengthwise is:
J = W x R2 ÷ 2g lnch-Lbs-Secs2 , in which:
W is total weight of the cylinder in pounds
R is outside radius of the cylinder in inches
g is acceleration of gravity, always 32.16

PRISM...
J (moment of inertia) of a prism of uniform cross section about the axis shown is:
J = W x (A2 + 82) ÷ 12g lnch-Lbs-Secs2, in which:
W is total weight of prism in pounds
A and B are cross section dimensions in inches
g is acceleration of gravity, always 32.16