Resistance to motion

This is the resistance a vehicle faces while attempting to move from a stall condition or while accelerating. This resistance must be overcome by the powerplant of the engine in order to sustain motion. When the power produced is smaller than the resistance to motion, the vehicle will gradually slow down. We must have experienced the slowing down of bicycles if we stop pedaling. The bicycle also slows down if we go uphill or if wind blows from front. A poorly inflated tire also causes the vehicle to groan more and slow down. These are the resistances that force the vehicle to slow down under their effect.

Broadly the resistances can be categorized into the following categories:

• Aerodynamic drag
• Gradient resistance
• Rolling resistance
• Inertia

All the above produce a restraining force working against the tractive force. The tractive force must be greater than or equal to the resistive forces in order to maintain a sustainable motion. We can balance them as

F = F _req = F_A + F_G + F_R + F_I

where

F_A= Force due to air resistance

F_G = Force due to gradient of a slope

F_G = Force due to rolling resistance

F_I = Force due to moving or static inertia

The last one F_I comes into the picture only when the vehicle accelerates or decelerates, while the first three always offer a resistance even when the vehicle is moving at a constant speed.

Air resistance/ Aerodynamic drag:

When a body travels within a dense medium, the molecules of the medium collide with the moving object and thereby absorb some of the energy. This is felt as a resistance to the moving object. If the medium is denser, then the resistance is more. Also when the object moves at a faster speed, the resistance increases proportionately. Mathematically it can be expressed as:

F_A = −½ × C_d × P × V²

where

C_d = Co−efficient of discharge

P = Pressure

V = Velocity of the vehicle

Gradient resistance:

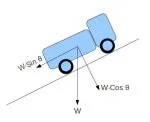
A truck moving uphill

When the vehicle travels uphill, a component of its weight works in a direction opposite to its motion. If some energy is not supplied to overcome this backward force, then the vehicle would slow down, stall and roll backwards. If the vehicle is trading uphill at a slope of θ, then the weight of the vehicle, W has two components: one perpendicular to the road surface (with a value W·Cos θ) and the other along the road surface (with a value W·Sin θ). The component along the road surface is the one that tries to restrict the motion.

The gradient resistance is given by: F_G = W·Sin θ

Rolling resistance

When a vehicle rolls, it rolls with its tires in contact with the road surface. The relative motion of two hard surfaces produces a friction. Further, neither the road, nor the tire are perfectly rigid. Hence, both flex under the load slightly. As there is a gradual deformation at the contact between the road and the tire, greatest at the bottom most point and least at the entry and exit points, the slip of the tire w.r.t. the road produces another type of loss of energy which results in a resistance.

Rolling resistance is composed of the following components:

• Tire Rolling resistance: F_R,T
• Road rolling resistance: F_R,Tr
• Resistance due to tire slip angle: F_R,α
• Resistance due to bearing friction and residual braking: F_R,fr

Hence the rolling resistance offered may be written as:

F_R = F_R,T + F_R,Tr + F_R,α + F_R,fr

The tire rolling resistance F_R,T is a result of the resistance due to flexure of the tire, air resistance on the tire and friction of tire with the road. These three can be summed up and written as:

F_R,T = F_R.T.flex + F_R.T.A + F_R.T.fr.

In a simplified manner the total rolling resistance can be related to the vertical load on the wheels and can be written as:

Co−efficient of rolling friction, k_R = ^F_R/_FZ.w