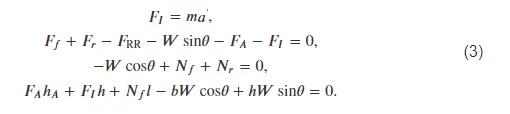
Classical Design of Gear Train
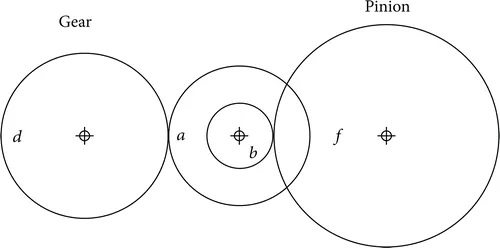
In order to find the required overall gear ratio, the compound gear train contains two pairs of gears, d-a and b-f (Figure 1). The desired gear ratio, itot, between the input and output gears is displayed as
|
|
where wo and wi are the angular velocities ofthe output andinput gears, respectively, and n expresses the number of teeth on each gear wheel.
Figure 1: Compound gear train.
Classical Gear Ratio Optimization
In the augmented Lagrangian multiplier method, the objective function is computing the number of teeth for gears d, a, b, and f in order to find a gear ratio, itot. The minimum number of teeth for each gear is assumed between 12 and 60. The target ratio, itrg, is assumed to be 1/6.93, and the function is expressed as follows:
|
|
In other words, the process is going to compute the optimum values of four variables that will minimize the squared difference between the target ratio, itrg, and available gear ratio, itot. The objective function is expressed as the squared error between the actual and the desired gear ratios.
An alternative solution for the gear train problem is founded by the differential evolution strategy. These solutions have been found to be globally optimal by applying explicit enumeration as mentioned in Tables 1 and .In this paper this problem has been resolved with genetic algorithm for 2009 hummer H3 4dr SUV.
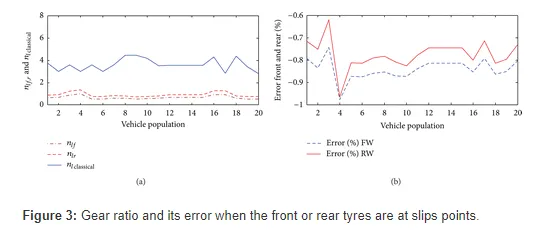
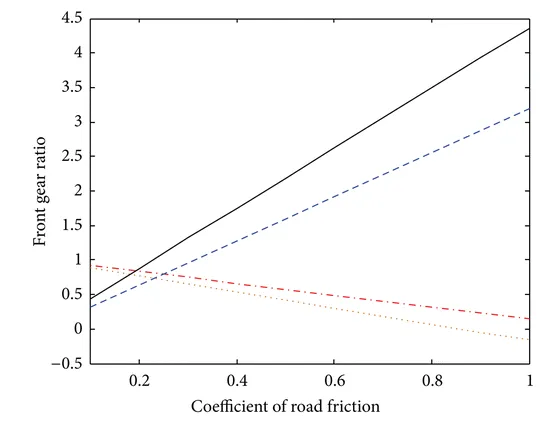
The dynamic gear ratio is obtained with applying dynamic equations as follows