
Process and Top 5 stages of Transportation Planning
Transportation planning is a complex problem. Increased facilities will change the environment and land use patterns and result in increased trips invalidating the original criteria and projections used. Increased use of operations research and systems approach to transportation planning in recent times seeks to optimise the system performance for deriving maximum benefit from the facilities.
The use of mathematical models to simulate the problem leads one to understand the variables involved to a reasonable degree; this helps in arriving at the best possible solution under a given set of circumstances.
Transport planning for urban areas and big cities is much more complex.
Urban transport planning process involves the following stages:
(i) Inventorying of existing conditions.
(ii) Forecasting future conditions including land use.
(iii) Evaluation of alternative plans based on cost-benefit analysis.
(iv) Adoption and implementation of a programme.
(v) Continuing study to assess the impact to help in future planning.
The following sequential stages are relevant to transportation planning:
A trip is a one-way movement of a person by a mechanised mode of transport, having an ‘origin’ (start of the trip) and a ‘destination’ (end of the trip). Trips may be home-based or non- home-based; in the former, one end of the trip – either the origin or the destination is at the home of the person while in the latter, neither end of the trip is the home of the person making the trip. The trip ends are classified as generations and attractions. In the case of home-based trips, the home end of any trip is a ‘generation’; in the case of non-home-based trips, the origin of the trip is a generation.
The non-home end of a home-based trip is an ‘attraction’; the destination of a non-based trip is also an attraction.
The following are the factors governing trip generation and attraction:
1. Family income – generally, the more the income, the higher will be the trip generation rate.
2. Car ownership – the more the households owning cars, the more the trip generation.
3. Family size and composition – the more the number of members and those who go out for work, the more the trips generated. Age structure is a significant factor. Young school-going children generate trips while elderly people do not.
4. Land-use characteristics have a bearing on trip generation.
5. Accessibility to a public transport system can generate more trips.
6. Employment opportunities, existence of shopping malls and offices influence the trip attraction rate.
7. In general, two approaches – multiple linear regression analysis and category analysis – are used for estimating trip generation.
Multiple Linear Regression Analysis:
This is a well-known statistical technique for connecting independent variables with a dependent variable using a mathematical relationship. The total number of trips is the dependent variable and the various measurable factors that influence trip generation are the independent variables.
The general form of the relationship is

Category Analysis:
Also called cross-classification technique, this considers trip-making by individual households rather than by the different zones. Households in the study area are divided into several categories, and their base year trip rates are determined by surveys.
Income-class is another variable; similarly car-ownership levels and household structures are other variables.
This method has a number of advantages over regression analysis. A multi-dimensional matrix is used to define the categories, each dimension representing one independent variable, which are again classified into a definite number of discrete class intervals. Unlike in regression analysis, no mathematical equation is derived, and the computations are relatively simple. Data from census can be used directly, saving considerable effort.
However, new variables cannot be easily introduced at a later stage, and large samples are needed to assign trip rates to any category.
Trips are made for different purposes, and a classification by purpose is helpful.
The following are some of the important classes based on the purpose of a trip:
v. Health and medical
vi. Social, recreational, and sports
vii. Miscellaneous purposes.
A typical distribution obtained by Central Road Research Institute (CRRI) is given below:

The above classification covers only home-based trips since these constitute 80 to 90% of the total number.
After estimating the trips generated from and attracted to the various zones, it is necessary to apportion the trips generated in every zone to the zones to which these trips are attracted. In other words, the trip distribution stage determines the number of trips, tij, which would originate at zone i and terminate at zone j.
There are two broad types of trip distribution methods:
(i) Growth Factor Methods:
Growth factor methods have been used earlier; but these have now been replaced by the more rational synthetic models. However, growth factor methods are still used for the study of small areas in view of their simplicity. These methods are based on the assumption that the existing travel patterns can be projected to a future design year by using certain growth factors.
Tij = tij X E … (4.54)
Where, Tij = Trips from zone i to zone j in the design year,
tij = Observed trips in the base year from zone i to zone j
and E = growth factor
E may be taken to be uniform or constant, or an average value may be used. Iterative methods have also been devised in this category.
(ii) Synthetic Methods:
Synthetic models are used to develop a relationship between trips, the resistance to travel between the zones, and the relative attractiveness of the zones for travel. Existing data are used for this purpose. Once the model is established, it can be used to predict future pattern of inter-zonal travel trips.
One of the well-known synthetic models is the gravity model. As proposed by Voorhees (1955), this model assumes that the interchange of trips between different zones of an area is dependent upon the relative attraction between the zones and their spatial separation, as measured by an appropriate function of the distance.
The relative attraction of each zone makes the trip maker overcome the spatial separation by his or her ability, desire or necessity. While the trip interchange is directly proportional to the relative attraction between the zones, it is inversely proportional to the measure of spatial separation. (This is somewhat similar to Newton’s Universal Law of Gravitation, and hence the name Gravity Model.)
The following simple equation represents this relationship –
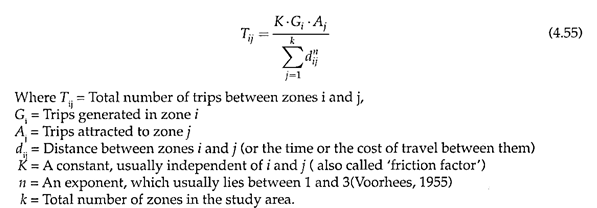
Existing data are used to calibrate the model parameters K and n, using a computer program. Assuming these parameters to be the same at a future date, the trip interchanges are computed by substituting the future trip generated values in the model.
This is the stage in which the trip interchanges are allocated to different parts of the network. The route between any two O and D-pairs to be used is determined and the inter-zonal flows are assigned to the selected routes.
All traffic assignment techniques are based on route selection, which is made on the basis of a number of criteria like the journey time, distance, cost, comfort, convenience and safety. Distance or journey time may often be considered as the sole criterion, but the problem of driver’s preferences is not always as simple as this. While for small jobs route selection may be made manually; for large jobs the use of the digital computer is a must.
A concept which is commonly used in traffic assignment is the Moore Algorithm, developed for dealing with phone calls that query for the shortest path between two points. The algorithm comes in handy in computer programmes developed for this purpose and helps in building the minimum-path tree between any two zone centroids in a street network.
The following are the traffic assignment methods normally used:
(i) ‘All-or-nothing’ method (Free or Desire assignment)
(ii) Multiple route method
(iii) Capacity restraint method
(iv) Diversion curves approach
‘All-or-Nothing’ Method:
In this method, all the trips between any O and D-pair are assigned to the shortest path between the trip ends. This is, in a way, oversimplifying the problem as it is based on the premise that the route followed by the traffic is the one with the least travel resistance, which can be measured in terms of the distance, travel time, cost, or a suitable combination of these factors. The traffic volumes of the trips are assigned based on the principle of minimum-path tree. Once the assignment is completed, it is checked to ensure that no link in the network is loaded beyond its capacity. In case of an overload, the journey time at the overloaded link increases, which calls for the repetition of the traffic assignment.
If a superior facility like an expressway is available, drivers tend to prefer to use this even though the route is longer. The ‘all-or-nothing’ method does not reflect small differences in journey time and may result in unrealistic route selection.
The other methods mentioned above are considered to be more accurate, but will need the use of a digital computer.
Mode split or Modal split is the process of separating trips by the mode of travel. In general, modal split refers to the trips made by private cars and the public transportation system – buses or trains.
The factors affecting the choice among alternative modes are not restricted to cost and time, but are heterogeneous.
Some broad categories are given below:
1. Characteristics of the trip – trip purpose, trip distance, etc.
2. Household characteristics – income, car ownership, family size and composition.
3. Zonal characteristics – residential density, concentration of workers, distance from the central business district.
4. Network characteristics – accessibility and travel time comparison by the different travel modes.
An understanding of the modal split is very relevant to transportation planning. Future transportation pattern can be accurate only if the motivations that guide the travellers in their choice of the modes of transportation can be analysed and understood. The problem being a complex one, better techniques are being evolved to aid the planning process.