Cam Design

The translational or rotational displacement of the follower is a function of the rotary angle of the cam. A designer can define the function according to the specific requirements in the design. The motion requirements, listed below, are commonly used in cam profile design.

Disk Cam with Knife-Edge Translating Follower

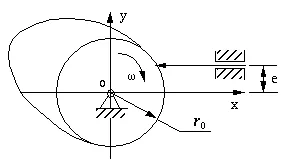
Figure 6-12 is a skeleton diagram of a disk cam with a knife-edge translating follower. We assume that the cam mechanism will be used to realize the displacement relationship between the rotation of the cam and the translation of the follower.

Figure 6-12 A Skeleton Diagram of disk cam with knife-edge translation

Below is a list of the essential parameters for the evaluation of these types of cam mechanisms. However, these parameters are adequate only to define a knife-edge follower and a translating follower cam mechanism.

Parameters:

r_o: The radius of the base circle;

e: The offset of the follower from the rotary center of the cam. Notice: it could be negative.

s: The displacement of the follower which is a function of the rotary angle of the cam -- .

IW: A parameter whose absolute value is 1. It represents the turning direction of the cam. When the cam turns clockwise: IW=+1, otherwise: IW=-1.

Cam profile design principle:

The method termed inversion is commonly used in cam profile design. For example, in a disk cam with translating follower mechanism, the follower translates when the cam turns. This means that the relative motion between them is a combination of a relative turning motion and a relative translating motion. Without changing this feature of their relative motion, imagine that the cam remains fixed. Now the follower performs both the relative turning and translating motions. We have inverted the mechanism.

Furthermore, imagine that the knife-edge of the follower moves along the fixed cam profile in the inverted mechanism. In other words, the knife edge of the follower draws the profile of the cam. Thus, the problem of designing the cam profile becomes a problem of calculating the trace of the knife edge of the follower whose motion is the combination of the relative turning and the relative translating.

Design equations:

Figure 6-13 Profile design of translating cam follower

In Figure 6-13, only part of the cam profile AK is displayed. Assume the cam turns clockwise. At the beginning of motion, the knife edge of the follower contacts the point of intersection A of the base circle and the cam profile. The coordinates of A are (So, e), and So can be calculated from equation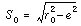 

Suppose the displacement of the follower is S when the angular displacement of the cam is . At this moment, the coordinates of the knife edge of the follower should be (So + S, e).

To get the corresponding position of the knife edge of the follower in the inverted mechanism, turn the follower around the center of the cam in the reverse direction through an angle of . The knife edge will be inverted to point K, which corresponds to the point on the cam profile in the inverted mechanism. Therefore, the coordinates of point K can be calculated with the following equation:

(6-5)

Note:

• The offset e is negative if the follower is located below the x axis.
• When the rotational direction of the cam is clockwise: IW = +1, otherwise: IW = -1.

6.5.2 Disk Cam with Oscillating Knife-Edge Follower

Suppose the cam mechanism will be used to make the knife edge oscillate. We need to compute the coordinates of the cam profile that results in the required motion of the follower.

Figure 6-14 Disk cam with knife-edge oscillating follower

The essential parameters in this kind of cam mechanisms are given below.

r_o: The radius of the base circle;

a: The distance between the pivot of the cam and the pivot of the follower.

l: The length of the follower which is a distance from its pivot to its knife edge.

: The angular displacement of the follower which is a function of the rotary angle of the cam -- .

IP: A parameter whose absolute value is 1. It represents the location of the follower. When the follower is located above the x axis: IP=+1, otherwise: IP=-1.

IW: A parameter whose absolute value is 1. It represents the turning direction of the cam. When the cam turns clockwise: IW=+1, otherwise: IW=-1.

Cam profile design principle

The fundamental principle in designing the cam profiles is still inversion, similar to that that for designing other cam mechanisms, (e.g., the translating follower cam mechanism). Normally, the follower oscillates when the cam turns. This means that the relative motion between them is a combination of a relative turning motion and a relative oscillating motion. Without changing this feature of their relative motion, let the cam remain fixed and the follower performs both the relative turning motion and oscillating motion. By imagining in this way, we have actually inverted the mechanism.

Figure 6-15 Cam profile design for a rotating follower

In Figure 6-15, only part of the cam profile BK is shown. We assume that the cam turns clockwise.

At the beginning of motion, the knife edge of the follower contacts the point of intersection (B) of the base circle and the cam profile. The initial angle between the follower (AB) and the line of two pivots (AO) is 0. It can be calculated from the triangle OAB.

When the angular displacement of the cam is , the oscillating displacement of the follower is  which measures from its own initial position. At this moment, the angle between the follower and the line passes through two pivots should be +0.

The coordinates of the knife edge at this moment will be

(6-6)

To get the corresponding knife-edge of the follower in the inverted mechanism, simply turn the follower around the center of the cam in the reverse direction of the cam rotation through an angle of . The knife edge will be inverted to point K which corresponds to the point on the cam profile in the inverted mechanism. Therefore, the coordinates of point K can be calculated with the following equation:

(6-7)

Note:

• When the initial position of the follower is above the x axis, IP = +1, otherwise: IP = -1.
• When the rotary direction of the cam is clockwise: IW = +1, otherwise: IW = -1.

6.5.3 Disk Cam with Roller Follower

Additional parameters:

• r: the radius of the roller.
• IM: a parameter whose absolute value is 1, indicating which envelope curve will be adopted.
• RM: inner or outer envelope curve. When it is an inner envelope curve: RM=+1, otherwise: RM=-1.

Design principle:

The basic principle of designing a cam profile with the inversion method is still used. However, the curve is not directly generated by inversion. This procedure has two steps:

1. Imagine the center of the roller as a knife edge. This concept is important in cam profile design and is called the trace point) of follower. Calculate the pitch curve aa, that is, the trace of the pitch point in the inverted mechanism.
2. The cam profile bb is a product of the enveloping motion of a series of rollers.

Figure 6-16 The trace point of the follower on a disk cam

Design equations:

The problem of calculating the coordinates of the cam profile is the problem of calculating the tangent points of a sequence of rollers in the inverted mechanism. At the moment shown Figure 6-17, the tangent point is P on the cam profile.

Figure 6-17 The tangent point, P, of a roller to the disk cam

The calculation of the coordinates of the point P has two steps:

1. Calculate the slope of the tangent tt of point K on pitch curve, aa.
2. Calculate the slope of the normal nn of the curve aa at point K.

Since we have already have the coordinates of point K: (x, y), we can express the coordinates of point P as

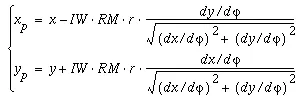
(6-8)