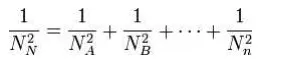EQUIVALENT STIFFNESS OF SPRING. 

(1) Springs in series

(2) Springs in parallel 

(3) Combined springs

(4) Inclined springs

DAMPING:

 It is the resistance to the motion of a vibrating body. The vibrations associated with this resistance are known as damped vibrations.

 Types of damping:

 (1) Viscous damping

 (2) Dry friction or coulomb damping

 (3) Solid damping or structural damping

4) Slip or interfacial damping.

Damping Coefficient: 

The damping force per unit velocity is known as damping coefficient.

Equivalent damping coefficient:

 Dampers may be connected either in series or in parallel to provide required damping.

 DAMPED VIBRATION: 

The vibrations associated with this resistance are known as damped vibrations.

 Damping factor:

 Damping factor can be defined as the ratio of actual damping coefficient to critical damping coefficient.

Logarithmic decrement:

 It is defined as the natural logarithm of ratio of any two successive amplitudes of an under damped system. It is a dimensionless quantity.

TRANSVERSE VIBRATION:

 When the particles of the shaft or disc moves approximately perpendicular to the axis of the shaft, then the vibrations known as transverse vibrations.

Whirling speed of shaft:

 The speed, at which the shaft runs so that the additional deflection of the shaft from the axis of rotation becomes infinite, is known as critical or whirling speed.

No shaft can ever be perfectly straight or perfectly balanced. When an element of mass is a distance from the axis of rotation, centrifugal force, will tend to pull the mass outward. The elastic properties of the shaft will act to restore the ―straightness‖. If the frequency of rotation is equal to one of the resonant frequencies of the shaft, whirling will occur. In order to save the machine from failure, operation at such whirling speeds must be avoided.

The whirling frequency of a symmetric cross section of a given length between two points is

given by:

Where E = young's modulus, I = Second moment of area, m = mass of the shaft, L= length of the shaft between points

A shaft with weights added will have an angular velocity of N (rpm) equivalent as follows: