FORCED VIBRATION WITH DAMPING:

 In this section we will see the behaviour of the spring mass damper model when we add a harmonic force in the form below. A force of this type could, for example, be generated by a rotating imbalance.

If we again sum the forces on the mass we get the following ordinary differential equation:

The steady state solution of this problem can be written as:

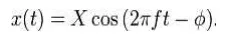
The result states that the mass will oscillate at the same frequency, f, of the applied force, but with a phase shift φ.

The amplitude of the vibration ―X‖ is defined by the following formula.

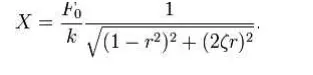
Where ―r‖ is defined as the ratio of the harmonic force frequency over the undamped natural frequency of the mass–spring–damper model.

 The phase shift , φ, is defined by the following formula.

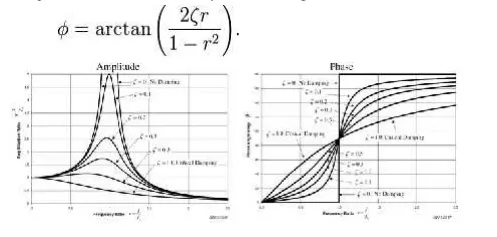
The plot of these functions, called "the frequency response of the system", presents one of the most important features in forced vibration. In a lightly damped system when the forcing frequency nears the natural frequency ( r ~= 1) the amplitude of the vibration can get extremely high. This phenomenon is called resonance (subsequently the natural frequency of a system is often referred to as the resonant frequency). In rotor bearing systems any rotational speed that excites a resonant frequency is referred to as a critical speed.

If  resonance  occurs  in  a  mechanical  system  it  can  be  very  harmful  – leading  to eventual failure of the system. Consequently, one of the major reasons for vibration analysis is to predict when this type of resonance may occur and then to determine what steps to take to prevent it from occurring. As the amplitude plot shows, adding damping can significantly reduce the magnitude of the vibration. Also, the magnitude can be reduced if the natural frequency can be shifted away from the forcing frequency by changing the stiffness or mass of the system. If the  system cannot  be  changed,  perhaps  the  forcing  frequency can  be  shifted  (for  example, changing the speed of the machine generating the force).

The following are some other points in regards to the forced vibration shown in the frequency response plots.

 At a given frequency ratio, the amplitude of the vibration, X, is directly proportional to the amplitude of the force F₀ (e.g. if you double the force, the vibration doubles)

 With little or no damping, the vibration is in phase with the forcing frequency when the frequency ratio r < 1 and 180 degrees out of phase when the frequency ratio r > 1

by the mass increases with the frequency. Since the deflection seen in the spring, X, is reduced in this region, the force transmitted by the spring (F = kx) to the base is reduced. Therefore the mass–spring–damper≫ system is isolating the harmonic force from the mounting base – referred to as vibration isolation. Interestingly, more damping actually reduces the effects of vibration isolation when r 1 because the damping force (F = cv) is also transmitted to the base.

  ROTATING UNBALANCE FORCED VIBRATION: 

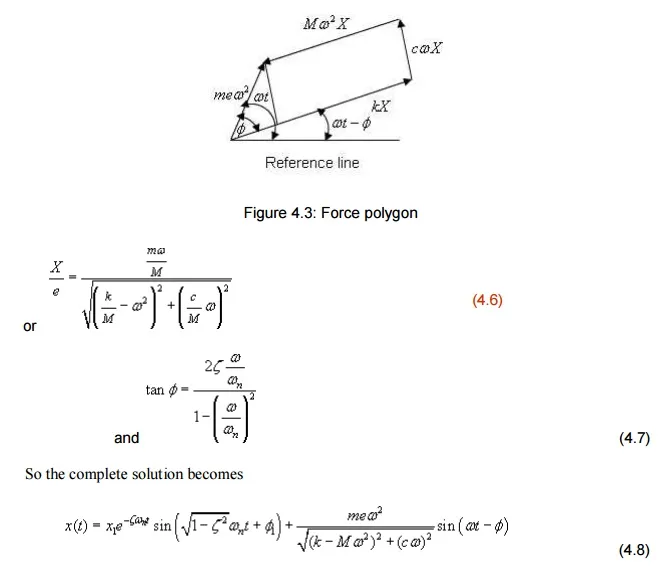
One may find many rotating systems in industrial applications. The unbalanced force in such a system can be represented by a mass m with eccentricity e , which is rotating with angular velocity as shown in Figure 4.1.

Figure 4.1 : Vibrating system with rotating unbalance

 Let x be the displacement of the nonrotating mass (M-m) from the static equilibrium position, then the displacement of the rotating mass m is  x+esinwt

 From the freebody diagram of the system shown in figure 4.2, the equation of motion is