FORCED VIBRATION

  INTRODUCTION:

 When a system is subjected continuously to time varying disturbances, the vibrations resulting under the presence of the external disturbance are referred to as forced vibrations.

 Forced vibration is when an alternating force or motion is applied to a mechanical system. Examples of this type of vibration include a shaking washing machine due to an imbalance, transportation vibration (caused by truck engine, springs, road, etc), or the vibration of a building during an earthquake. In forced vibration the frequency of the vibration is the frequency of the force or motion applied, with order of magnitude being dependent on the actual mechanical system.

 When a vehicle moves on a rough road, it is continuously subjected to road undulations causing the system to vibrate (pitch, bounce, roll etc). Thus the automobile is said to undergo forced vibrations. Similarly whenever the engine is turned on, there is a resultant residual unbalance force that is transmitted to the chassis of the vehicle through the engine mounts, causing again forced vibrations of the vehicle on its chassis. A building when subjected to time varying ground motion (earthquake) or wind loads, undergoes forced vibrations. Thus most of the practical examples of vibrations are indeed forced vibrations.

CAUSES RESONANCE:

 Resonance is  simple to  understand  if  you  view the spring and  mass  as  energy storage

elements – with the mass storing kinetic energy and the spring storing potential energy. As discussed earlier, when the mass and spring have no force acting on them they transfer energy back and forth at a rate equal to the natural frequency. In other words, if energy is to be efficiently pumped into both the mass and spring the energy source needs to feed the energy in at a rate equal to the natural frequency. Applying a force to the mass and spring is similar to pushing a child on swing, you need to push at the correct moment if you want the swing to get higher and higher. As in the case of the swing, the force applied does not necessarily have to be high to get large motions; the pushes just need to keep adding energy into the system.

The damper, instead of storing energy, dissipates energy. Since the damping force is proportional to the velocity, the more the motion, the more the damper dissipates the energy. Therefore a point will come when the energy dissipated by the damper will equal the energy being fed in by the force. At this point, the system has reached its maximum amplitude and will continue to vibrate at this level as long as the force applied stays the same. If no damping exists, there is nothing to dissipate the energy and therefore theoretically the motion will continue to grow on into infinity.

   FORCED VIBRATION OF A SINGLE DEGREE-OF-FREEDOM SYSTEM:

 We saw that when a system is given an initial input of energy, either in the form of an initial displacement or an initial velocity, and then released it will, under the right conditions, vibrate freely. If there is damping in the system, then the oscillations die away. If a system is given a continuous input of energy in the form of a continuously applied force or a continuously applied displacement, then the consequent vibration is called forced vibration. The energy input can overcome that dissipated by damping mechanisms and the oscillations are sustained.

We will consider two types of forced vibration. The first is where the ground to which the system is attached is itself undergoing a periodic displacement, such as the vibration of a building in an earthquake. The second is where a periodic force is applied to the mass, or object performing the motion; an example might be the forces exerted on the body of a car by the forces produced in the engine. The simplest form of periodic force or displacement is sinusoidal, so we will begin by considering forced vibration due to sinusoidal motion of the ground. In all real systems, energy will be dissipated, i.e. the system will be damped, but often the damping is very small. So let us first analyze systems in which there is no damping.

STEADY STATE RESPONSE DUE TO HARMONIC OSCILLATION:

 Consider a spring-mass-damper system as shown in figure 4.1. The equation of motion of this system subjected to a harmonic force Fsin(wt) can be given by

where, m , k and c are the mass, spring stiffness and damping coefficient of the system, F is the amplitude of the force, w is the excitation frequency or driving frequency.

 Figure 4.2: Force polygon

 The steady state response of the system can be determined by solving equation(4.1) in many different ways. Here a simpler graphical method is used which will give physical understanding to this dynamic problem. From solution of differential equations it is known that the steady state solution (particular integral) will be of the form

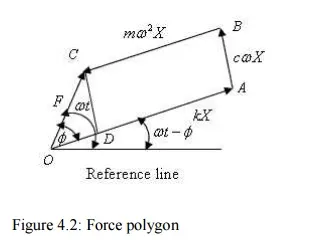
As each term of equation (4.1) represents a forcing term viz., first, second and third terms, represent the inertia force, spring force, and the damping forces. The term in the right hand side of equation (4.1) is the applied force. One may draw a close polygon as shown in figure 4.2 considering the equilibrium of the system under the action of these forces. Considering a reference line these forces can be presented as follows.

From equation (1), the resultant of the spring force, damping force and the inertia force will be the applied force, which is clearly shown in figure 4.2.

It may be noted that till now, we don't know about the magnitude of X and $  which can be easily computed from Figure 2. Drawing a line CD parallel to AB, from the triangle OCD of Figure 2,