
Gears And Trains
Introduction: The slip and creep in the belt or rope drives is a common phenomenon, in the transmission of motion or power between two shafts. The effect of slip is to reduce the velocity ratio of the drive. In precision machine, in which a definite velocity ratio is importance (as in watch mechanism, special purpose machines..etc), the only positive drive is by means of gears or toothed wheels.
Friction Wheels: Kinematiclly, the motion and power transmitted by gears is equivalent to that transmitted by friction wheels or discs in contact with sufficient friction between them. In order to understand motion transmitted by two toothed wheels, let us consider the two discs placed together.
When one of the discs is rotated, the other disc will be rotate as long as the tangential force exerted by the driving disc does not exceed the maximum frictional resistance between the two discs. But when the tangential force exceeds the frictional resistance, slipping will take place between the two discs. Thus the friction drive is not positive a drive, beyond certain limit.
Gears are machine elements that transmit motion by means of successively engaging teeth. The gear teeth act like small levers. Gears are highly efficient (nearly 95%) due to primarily rolling contact between the teeth, thus the motion transmitted is considered as positive.
Gears essentially allow positive engagement between teeth so high forces can be transmitted while still undergoing essentially rolling contact. Gears do not depend on friction and do best when friction is minimized.
Gears are used to change speed in rotational movement.

In the example above the blue gear has eleven teeth and the orange gear has twenty five. To turn the orange gear one full turn the blue gear must turn 25/11 or 2.2727r turns. Notice that as the blue gear turns clockwise the orange gear turns anti-clockwise. In the above example the number of teeth on the orange gear is not divisible by the number of teeth on the blue gear. This is deliberate. If the orange gear had thirty three teeth then every three turns of the blue gear the same teeth would mesh together which could cause excessive wear. By using none divisible numbers the same teeth mesh only every seventeen turns of the blue gear.

A gear or cogwheel is a rotating machine part having cut teeth, or cogs, which mesh with another toothed part to transmit torque. Geared devices can change the speed, torque, and direction of a power source. Gears almost always produce a change in torque, creating a mechanical advantage, through their gear ratio, and thus may be considered a simple machine. The teeth on the two meshing gears all have the same shape. Two or more meshing gears, working in a sequence, are called a gear train or a transmission. A gear can mesh with a linear toothed part, called a rack, thereby producing translation instead of rotation.
The gears in a transmission are analogous to the wheels in a crossed belt pulley system. An advantage of gears is that the teeth of a gear prevent slippage.
When two gears mesh, if one gear is bigger than the other, a mechanical advantage is produced, with the rotational speeds, and the torques, of the two gears differing in proportion to their diameters.
In transmissions with multiple gear ratios—such as bicycles, motorcycles, and cars—the term "gear" as in "first gear" refers to a gear ratio rather than an actual physical gear. The term describes similar devices, even when the gear ratio is continuous rather than discrete, or when the device does not actually contain gears, as in a continuously variable transmission.
Fundamental Law of Gear-Tooth
Pitch point divides the line between the line of centers and its positiond ecides the velocity ratio of the two teeth. The above expression is the fundamental law of gear-tooth action.

Formation of teeth:
· Involute teeth
· Cycloidal teeth
Involute curve:
The curve most commonly use d for gear-tooth profiles is the involute of a circle. This involute curve is the path traced by a point on a line as the line Rolls without slipping on the circumference of a circle. It may also be defined asapathtraced by the end of a string, which is originally wrapped on a circle when the string is un wrapped from the circle. The circle from which the involute is derived is called the base circle

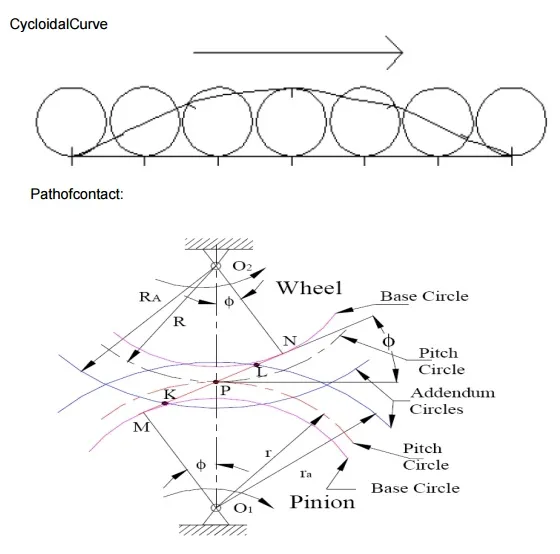
Consider a pinion driving wheel as shown in figure. When the pinion rotates in clockwise, the contact between a pair of involute teeth begin sat K(on the near the base circle of pinion or the outer end of the tooth face on the wheel ) and end sat L (outer end of the tooth face on the pinion or on the flank near the base circle of wheel).
MN is the common normal at the point of contacts and the common tangent to the base circles. The point K is the intersection of the addendum circle of wheel and the common tangent. The point L is the intersection of the addendum circle of pinion and common tangent.
The length of path of contact is the length of common normal cut-off by theaddendum circles of the wheel and the pinion. Thus the length of part of contact is KL which is the sum of the parts of path of contacts KP and PL. Contact length KP is called as path of approach and contact length PL is called as path of recess.

Arc of contact: Arc of contact is the path traced by a point on the pitch circle from the beginning to the end of engagement of a given pair of teeth. In Figure, the arc of contact is EPF or GPH.
The arc GP is known as arc of approach and the arc PH is called arc of recess. The angles subtended by these arcs at O1 are called angle of approach and angle of recess respectively.

Contact Ratio ( or Number of Pairs of Teeth in Contact)
The contact ratio or the number of pairs of teeth in contact is defined as the ratio of the length of the arc of contact to the circular pitch.

Continuous motion transfer requires two pairs of teeth in contact at the ends of the path of contact, though the reisonly one pair in contact in the middle of the path, as in Figure. The average number of teeth in contact is an important parameter-If it is tool owdue the use of inappropriate profile shift sortoan excessive centre distance. Them anufacturinginaccuracies may lead to loss of kinematic continuity-that is to impact, vibration and noise The average number of teeth in contact is also a guide tolod sharing between teeth; it is termed the contact ratio.

The tooth tip of the pinion will then undercut the tooth on the wheel at the root and damages part of the involute profile. This effect is known as interference, and occurs when the teeth are being cut and weakens the tooth at its root.
In general, the phenomenon, when the tip of tooth undercuts the root on its mating gear is known as interference.
Similarly, if the radius of the addendum circles of the wheel increases beyond O2M, then the tip of tooth on wheel will cause interference with the tooth on pinion. The points M and N are called interference points.
Interference may be avoided if the path of the contact does not extend beyond interference points. The limiting value of the radius of the addendum circle of the pinion is O1N and of the wheel is O2M.
The interference may only be prevented, if the point of contact between the two teeth is always on the involute profiles and if the addendum circles of the two mating gears cut the common tangent to the base circles at the points of tangency.
When interference is just prevented, the maximum length of path of contact is MN.
Methods to avoid Interference
1. Height of the teeth may be reduced.
2.Under cut of the radial flank of the pinion.
3.Centre distance may be increased. It leads to increase in pressure angle.
4. By tooth correction, the pressure angle, centre distance and base circles remain unchanged, but tooth thickness of gear will be greater than the pinion tooth thickness.
Minimum number of teeth on the pinion avoid Interference
The pinion turns clockwise and drives the gear as shown in Figure.
Points M and N are called interference points. i.e., if the contact takes place beyond M and N, interference will occur.
The limiting value of addendum circle radius of pinion is O1N and the limiting value of addendum circle radius of gear is O2M. Considering the critical addendum circle radius of gear, the limiting number of teeth on gear can be calculated.
Let
Ф = pressure angle
R = pitch circle radius of gear = ½ mT
r = pitch circle radius of pinion = ½ mt
T & t = number of teeth on gear & pinion
m = module

