Torsional Shear Stress 

When a machine member is subjected to the action of two equal and opposite couples acting in parallel planes (or torque or twisting moment), then the machine member is said to be subjected to torsion. The stress set up by torsion is known as torsional shear stress. It is zero at the centroidal axis and maximum at the outer surface.

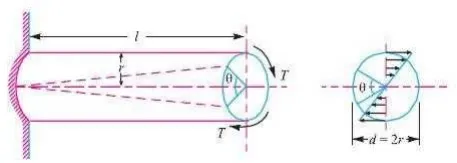
Consider a shaft fixed at one end and subjected to a torque (T) at the other end as shown in Fig. As a result of this torque, every cross-section of the shaft is subjected to torsional shear stress. We have discussed above that the torsional shear stress is zero at the centroidal axis and maximum at the outer surface. The maximum torsional shear stress at the outer surface of the shaft may be obtained from the following equation:

(τ /r) = (T/J) = (Cθ/ l )

where

τ    = Torsional shear stress induced at the outer surface of the shaft or maximum shear stress,

               = Radius of the shaft,

= Torque or twisting moment,

= Second moment of area of the section about its polar axis or polar moment of inertia,

C = Modulus of rigidity for the shaft material, l = Length of the shaft, and

               = Angle of twist in radians on a length l.