RMS Voltage of AC Waveform
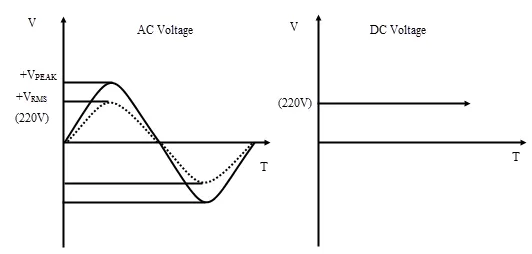
An alternating waveform or AC waveform, which is associated with the AC current, is a periodic waveform that alternates between the positive and the negative values. Sine or Sinusoidal wave is the most common time varying wave that is used to represent an AC waveform.
In case of DC, the values of voltage and current are generally stable over time. It is easy to express the magnitude of voltage or current i.e. how much voltage or current is present in any part of the circuit.
In case of AC, unlike DC, they can’t be characterized by one magnitude as the amplitude of an AC waveform is continuously varying with time.
There are many ways to represent the magnitude of an AC waveform. Some of them are
· Instantaneous value
· Peak value
· Peak to peak value
· Average value
· RMS value
In previous sections, we have seen about the average voltage value and instantaneous values of an AC waveform. Here, another important topic about the AC waveform, RMS Voltage of an AC waveform is described.
RMS means “Root Mean Squared” value.The RMS voltage is defined as the “Square root of the averages of the squares of all instantaneous voltages in the wave form”. RMS value can be found as follows, the input is squared and the average value is calculated.
This gives the average power. In order to calculate the voltage, square root of the previously obtained average value is taken. Hence, it is called as Root-Mean-Squared voltage.
RMS value is used to obtain the DC equivalent of AC that would dissipate same amount of heat when either values are applied to a resistor. An Alternating current with a maximum value of 1.4 Amperes will produce a same heat through a resistor as a DC current of 1 Ampere.
Hence, RMS value is also sometimes known as Equivalent or DC Equivalent value. RMS measurement of voltage or current of an AC waveform is the best way to relate AC and DC quantities.
RMS value is also called as ‘Effective Value’ which is the equivalent of the DC value, either current or voltage, that the alternating signal produces a same power as DC.
Generally, the mains voltage is actually the RMS value. In India, for example, the supply voltage is between 220-240V. This is actually the RMS value of the AC which is equivalent to producing same power as 220-240V DC.

RMS is used to refer only AC waveforms i.e. time varying sinusoidal waveforms like AC voltage, AC current or other complex waveforms where the magnitude changes with time. RMS is not applicable to DC circuits where the magnitude is constant with time.
The process of finding the RMS voltage is very much similar to the process of the average voltage value. There are two methods to find the RMS voltage of a waveform. They are: Graphical method and Analytical method.
In this method, we will find the RMS voltage value by using the mid ordinates or the instantaneous voltage values of the Alternating wave form.
The clear derivation of the RMS value is involved in multiple steps shown below.
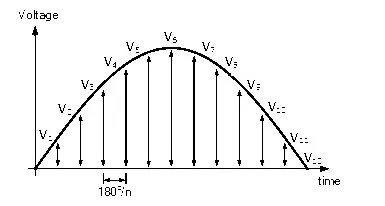
In every AC wave form, we have many instantaneous voltages and the number of instantaneous voltages is dependent on the timing durations. For example, if the waveform is divided into n mid-ordinates, then at an instance of time t = 2, the instantaneous voltage of the AC wave form is V2.
Similarly, at the instance, t = n, the instantaneous voltage is van, etc. So first we find the instantaneous voltage values of every instance of the periodic waveform, like V1, V2, V3, and Vn.
In order to find the RMS voltage of the wave form, we should find the square values of every voltage value of the AC wave form. This gives the ‘Square’ part of the RMS.
V12+V22+V32+V42+—-
Finding the mean or average of the sum of the squares of the voltage values. We divide the sum of squares by number of mid-ordinates. This gives the ‘Mean’ part of the RMS.
The average all voltage values of the AC wave form of periodic wave form, will give us the most accurate value of the RMS voltage. Generally, in all mathematical approximations, we establish the average values to keep off the fault values and to set out the most exact value of a computation.
If we have Vn values of voltages at n instances, the average is calculated as below.
The square root of this value gives us the RMS value of the AC wave form. The formula for calculating the RMS voltage value is shown below.

Where n is the number of instances,
V1, V2, V3, V4 …. are the instantaneous voltage values of the waveform.
Example
If we have an alternating waveform of maximum amplitude 20 Volts, let’s find its RMS voltage.
We divide the waveform into 10 mid – ordinate values as follows.

Therefore the RMS voltage of the AC wave form with 20V peak is 14.15 volts
Graphical method is a very effective method for finding the RMS values of all types of waveforms including complex waveforms.
Another method used to find the RMS voltage (or current) of the periodic AC waveform is Analytical method or Mathematical. This method is suitable for sinusoidal shaped wave forms.
In this method, we will calculate the RMS voltage by analysing the area under the curve of the AC waveform. This method is easier than Graphical method when dealing with pure sinusoidal waveforms.
A periodic sine wave signal with time period T is given by the expression
V (t) = Vm.cos (ωt)
Where ω = 2π / T
The RMS voltage can be calculated as
VRMS = √[1/T ∫0t Vm2 cos2(ωt) dt]
For one complete cycle or period of the wave form, the integration limits are 0 to 3600. So integrating through the lower and higher limits, we get
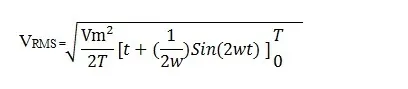
The complex equation can be further simplified by dividing it with ω = 2π / T. Then, the reduced equation for the RMS voltage is
VRMS = Vm/2 = Vm*0.707
The RMS voltage is calculated by using other voltage values of the waveform like peak voltage, peak to peak voltage and average voltages.
The RMS voltage of an alternating wave form is 0.707 times or 1 / √2 times of the peak voltage value. The RMS can be calculated by dividing the peak voltage by the square root of 2 (nearly 0.707).
VRMS = VPEAK x 1 /√2
VRMS = VPEAK x 0.707
The RMS voltage value can be calculated by multiplying the peak to peak voltage value with 1 / 2Ö2 or 0.35355. The peak to peak voltage is represented as VP-P.
VRMS = VP-P x 1 / 2√2
VRMS = VP-P x 0.353
The RMS voltage of an alternating wave form is 1.1107 times to that of average voltage value.
VRMS = VAVG x π / 2√2
VRMS = VAVG x 1.1107
· In case of alternating currents, the magnitudes of the current are expressed in the form of RMS values.
· In general, we say that the household supply voltage is about 220 Volts AC. This actually means the RMS voltage of household supply is 220 V.
· RMS value gives the DC equivalent values of AC waveform.
· All measuring equipment like Ammeters and Voltmeters measure the RMS only. In some expensive voltmeters, first the peak voltage is calculated and then multiplying it by 0.707, we get the RMS voltage value, most accurately.
· The RMS value is used to find the Crest factor and Form factor of the AC waveform, which are the key factors to decide the system performance.
For an AC waveform like sinusoidal waveform, RMS value, peak value and average value are the three important values that describe the magnitude. These three values are dependent on each other.
Apart from these three quantities, there are some ratios that are commonly defined between these three fundamental measurements. They are Form Factor and Peak (or Crest) factor.
“The Form factor is the ratio of the RMS voltage value of an alternating waveform to its average voltage”.
Form factor is represented by Kf.
Form factor = RMS voltage / average voltage
Kf = VRMS / VAVG
From the relation between average voltage value and the RMS value of a sinusoidal AC waveform to the peak (or max) value, we can calculate the form factor as
Kf = 0.707 VMAX / 0.637 VMAX
= 1.11
“The Crest factor is the ratio of peak voltage value to its RMS voltage value”. We also call this as “Peak factor” or “Amplitude factor”.
Crest factor is represented by KP.
Crest factor = Peak voltage / RMS voltage
KP = VPEAK (or VMAX) / VRMS
From the relation between the peak value and the RMS value, we can calculate the Crest factor as
KP = VMAX / 0.707 VMAX
= 1.414