Independent vs. dependent variables

When you are testing a cause-and-effect relationship, the variable that causes the relationship is called the independent variable and you plot it on the X axis, while the effect is called the dependent variable and you plot it on the Y axis. In some experiments you set the independent variable to values that you have chosen; for example, if you're interested in the effect of temperature on calling rate of frogs, you might put frogs in temperature chambers set to 10°C, 15°C, 20°C, etc. In other cases, both variables exhibit natural variation, but any cause-and-effect relationship would be in one way; if you measure the air temperature and frog calling rate at a pond on several different nights, both the air temperature and the calling rate would display natural variation, but if there's a cause-and-effect relationship, it's temperature affecting calling rate; the rate at which frogs call does not affect the air temperature.

Sometimes it's not clear which is the independent variable and which is the dependent, even if you think there may be a cause-and-effect relationship. For example, if you are testing whether salt content in food affects blood pressure, you might measure the salt content of people's diets and their blood pressure, and treat salt content as the independent variable. But if you were testing the idea that high blood pressure causes people to crave high-salt foods, you'd make blood pressure the independent variable and salt intake the dependent variable.

Sometimes, you're not looking for a cause-and-effect relationship at all, you just want to see if two variables are related. For example, if you measure the range-of-motion of the hip and the shoulder, you're not trying to see whether more flexible hips cause more flexible shoulders, or more flexible shoulders cause more flexible hips; instead, you're just trying to see if people with more flexible hips also tend to have more flexible shoulders, presumably due to some factor (age, diet, exercise, genetics) that affects overall flexibility. In this case, it would be completely arbitrary which variable you put on the X axis and which you put on the Y axis.

Fortunately, the P value and the r² are not affected by which variable you call the X and which you call the Y; you'll get mathematically identical values either way. The least-squares regression line does depend on which variable is the X and which is the Y; the two lines can be quite different if the r² is low. If you're truly interested only in whether the two variables covary, and you are not trying to infer a cause-and-effect relationship, you may want to avoid using the linear regression line as decoration on your graph.

Researchers in a few fields traditionally put the independent variable on the Y axis. Oceanographers, for example, often plot depth on the Y axis (with 0 at the top) and a variable that is directly or indirectly affected by depth, such as chlorophyll concentration, on the X axis. I wouldn't recommend this unless it's a really strong tradition in your field, as it could lead to confusion about which variable you're considering the independent variable in a linear regression.

How the test works

The graph shows the data points (dots), linear regression line (thick line), and data points connected to the point on the regression line with the same X value (thin lines). The regression line is the line that minimizes the sum of the squared vertical distances between the points and the line.

Regression line

Linear regression finds the line that best fits the data points. There are actually a number of different definitions of "best fit," and therefore a number of different methods of linear regression that fit somewhat different lines. By far the most common is "ordinary least-squares regression"; when someone just says "least-squares regression" or "linear regression" or "regression," they mean ordinary least-squares regression.

In ordinary least-squares regression, the "best" fit is defined as the line that minimizes the squared vertical distances between the data points and the line. For a data point with an X value of X₁ and a Y value of Y₁, the difference between Y₁ and Ŷ₁ (the predicted value of Y at X₁) is calculated, then squared. This squared deviate is calculated for each data point, and the sum of these squared deviates measures how well a line fits the data. The regression line is the one for which this sum of squared deviates is smallest. I'll leave out the math that is used to find the slope and intercept of the best-fit line; you're a biologist and have more important things to think about.

The equation for the regression line is usually expressed as Ŷ=a+bX, where a is the Y intercept and b is the slope. Once you know a and b, you can use this equation to predict the value of Y for a given value of X. For example, the equation for the heart rate-speed experiment is rate=63.357+3.749×speed. I could use this to predict that for a speed of 10 kph, my heart rate would be 100.8 bpm. You should do this kind of prediction within the range of X values found in the original data set (interpolation). Predicting Y values outside the range of observed values (extrapolation) is sometimes interesting, but it can easily yield ridiculous results if you go far outside the observed range of X. In the frog example below, you could mathematically predict that the inter-call interval would be about 16 seconds at −40°C. Actually, the inter-calling interval would be infinity at that temperature, because all the frogs would be frozen solid.

Sometimes you want to predict X from Y. The most common use of this is constructing a standard curve. For example, you might weigh some dry protein and dissolve it in water to make solutions containing 0, 100, 200 … 1000 µg protein per ml, add some reagents that turn color in the presence of protein, then measure the light absorbance of each solution using a spectrophotometer. Then when you have a solution with an unknown concentration of protein, you add the reagents, measure the light absorbance, and estimate the concentration of protein in the solution.

There are two common methods to estimate X from Y. One way is to do the usual regression with X as the independent variable and Y as the dependent variable; for the protein example, you'd have protein as the independent variable and absorbance as the dependent variable. You get the usual equation, Ŷ=a+bX, then rearrange it to solve for X, giving you X̂=(Y−a)/b. This is called "classical estimation."

The other method is to do linear regression with Y as the independent variable and X as the dependent variable, also known as regressing X on Y. For the protein standard curve, you would do a regression with absorbance as the X variable and protein concentration as the Y variable. You then use this regression equation to predict unknown values of X from Y. This is known as "inverse estimation."

Several simulation studies have suggested that inverse estimation gives a more accurate estimate of X than classical estimation (Krutchkoff 1967, Krutchkoff 1969, Lwin and Maritz 1982, Kannan et al. 2007), so that is what I recommend. However, some statisticians prefer classical estimation (Sokal and Rohlf 1995, pp. 491-493). If the r² is high (the points are close to the regression line), the difference between classical estimation and inverse estimation is pretty small. When you're construction a standard curve for something like protein concentration, the r² is usually so high that the difference between classical and inverse estimation will be trivial. But the two methods can give quite different estimates of X when the original points were scattered around the regression line. For the exercise and pulse data, with an r² of 0.98, classical estimation predicts that to get a pulse of 100 bpm, I should run at 9.8 kph, while inverse estimation predicts a speed of 9.7 kph. The amphipod data has a much lower r² of 0.25, so the difference between the two techniques is bigger; if I want to know what size amphipod would have 30 eggs, classical estimation predicts a size of 10.8 mg, while inverse estimation predicts a size of 7.5 mg.

Sometimes your goal in drawing a regression line is not predicting Y from X, or predicting X from Y, but instead describing the relationship between two variables. If one variable is the independent variable and the other is the dependent variable, you should use the least-squares regression line. However, if there is no cause-and-effect relationship between the two variables, the least-squares regression line is inappropriate. This is because you will get two different lines, depending on which variable you pick to be the independent variable. For example, if you want to describe the relationship between thumb length and big toe length, you would get one line if you made thumb length the independent variable, and a different line if you made big-toe length the independent variable. The choice would be completely arbitrary, as there is no reason to think that thumb length causes variation in big-toe length, or vice versa.

A number of different lines have been proposed to describe the relationship between two variables with a symmetrical relationship (where neither is the independent variable). The most common method is reduced major axis regression (also known as standard major axis regression or geometric mean regression). It gives a line that is intermediate in slope between the least-squares regression line of Y on X and the least-squares regression line of X on Y; in fact, the slope of the reduced major axis line is the geometric mean of the two least-squares regression lines.

While reduced major axis regression gives a line that is in some ways a better description of the symmetrical relationship between two variables (McArdle 2003, Smith 2009), you should keep two things in mind. One is that you shouldn't use the reduced major axis line for predicting values of X from Y, or Y from X; you should still use least-squares regression for prediction. The other thing to know is that you cannot test the null hypothesis that the slope of the reduced major axis line is zero, because it is mathematically impossible to have a reduced major axis slope that is exactly zero. Even if your graph shows a reduced major axis line, your P value is the test of the null that the least-square regression line has a slope of zero.

Coefficient of determination (r²)

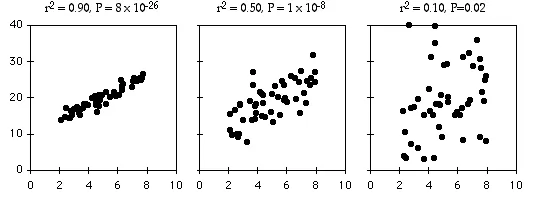
Three relationships with the same slope, same intercept, and different amounts of scatter around the best-fit line.

The coefficient of determination, or r², expresses the strength of the relationship between the X and Y variables. It is the proportion of the variation in the Y variable that is "explained" by the variation in the X variable. r² can vary from 0 to 1; values near 1 mean the Y values fall almost right on the regression line, while values near 0 mean there is very little relationship between X and Y. As you can see, regressions can have a small r² and not look like there's any relationship, yet they still might have a slope that's significantly different from zero.

To illustrate the meaning of r², here are six pairs of X and Y values:

If you didn't know anything about the X value and were told to guess what a Y value was, your best guess would be the mean Y; for this example, the mean Y is 10. The squared deviates of the Y values from their mean is the total sum of squares, familiar from analysis of variance. The vertical lines on the left graph below show the deviates from the mean; the first point has a deviate of 8, so its squared deviate is 64, etc. The total sum of squares for these numbers is 64+1+1+1+16+25=108.

Deviations from the mean Y and from the regression line.

If you did know the X value and were told to guess what a Y value was, you'd calculate the regression equation and use it. The regression equation for these numbers is Ŷ=2.0286+1.5429X, so for the first X value you'd predict a Y value of 2.0286+1.5429×1=3.5715, etc. The vertical lines on the right graph above show the deviates of the actual Y values from the predicted Ŷ values. As you can see, most of the points are closer to the regression line than they are to the overall mean. Squaring these deviates and taking the sum gives us the regression sum of squares, which for these numbers is 10.8.

The regression sum of squares is 10.8, which is 90% smaller than the total sum of squares (108). This difference between the two sums of squares, expressed as a fraction of the total sum of squares, is the definition of r². In this case we would say that r²=0.90; the X variable "explains" 90% of the variation in the Y variable.

The r² value is formally known as the "coefficient of determination," although it is usually just called r². The square root of r², with a negative sign if the slope is negative, is the Pearson product-moment correlation coefficient, r, or just "correlation coefficient." You can use either r or r² to describe the strength of the association between two variables. I prefer r², because it is used more often in my area of biology, it has a more understandable meaning (the proportional difference between total sum of squares and regression sum of squares), and it doesn't have those annoying negative values. You should become familiar with the literature in your field and use whichever measure is most common. One situation where r is more useful is if you have done linear regression/correlation for multiple sets of samples, with some having positive slopes and some having negative slopes, and you want to know whether the mean correlation coefficient is significantly different from zero; see McDonald and Dunn (2013) for an application of this idea.

Test statistic

The test statistic for a linear regression is t_s=√ d.f.×r² /√ (1−r²) . It gets larger as the degrees of freedom (n−2) get larger or the r² gets larger. Under the null hypothesis, the test statistic is t-distributed with n−2 degrees of freedom. When reporting the results of a linear regression, most people just give the r² and degrees of freedom, not the t_s value. Anyone who really needs the t_s value can calculate it from the r² and degrees of freedom.

For the heart rate–speed data, the r² is 0.976 and there are 9 degrees of freedom, so the t_s-statistic is 19.2. It is significant (P=1.3×10^-8).

Some people square t_s and get an F-statistic with 1 degree of freedom in the numerator and n−2 degrees of freedom in the denominator. The resulting P value is mathematically identical to that calculated with t_s.

Because the P value is a function of both the r² and the sample size, you should not use the P value as a measure of the strength of association. If the correlation of A and B has a smaller P value than the correlation of A and C, it doesn't necessarily mean that A and B have a stronger association; it could just be that the data set for the A–B experiment was larger. If you want to compare the strength of association of different data sets, you should use r or r².

Assumptions

Normality and homoscedasticity. Two assumptions, similar to those for anova, are that for any value of X, the Y values will be normally distributed and they will be homoscedastic. Although you will rarely have enough data to test these assumptions, they are often violated.

Fortunately, numerous simulation studies have shown that regression and correlation are quite robust to deviations from normality; this means that even if one or both of the variables are non-normal, the P value will be less than 0.05 about 5% of the time if the null hypothesis is true (Edgell and Noon 1984, and references therein). So in general, you can use linear regression/correlation without worrying about non-normality.

Sometimes you'll see a regression or correlation that looks like it may be significant due to one or two points being extreme on both the x and y axes. In this case, you may want to use Spearman's rank correlation, which reduces the influence of extreme values, or you may want to find a data transformation that makes the data look more normal. Another approach would be analyze the data without the extreme values, and report the results with or without them outlying points; your life will be easier if the results are similar with or without them.

When there is a significant regression or correlation, X values with higher mean Y values will often have higher standard deviations of Y as well. This happens because the standard deviation is often a constant proportion of the mean. For example, people who are 1.5 meters tall might have a mean weight of 50 kg and a standard deviation of 10 kg, while people who are 2 meters tall might have a mean weight of 100 kg and a standard deviation of 20 kg. When the standard deviation of Y is proportional to the mean, you can make the data be homoscedastic with a log transformation of the Y variable.

Linearity. Linear regression and correlation assume that the data fit a straight line. If you look at the data and the relationship looks curved, you can try different data transformations of the X, the Y, or both, and see which makes the relationship straight. Of course, it's best if you choose a data transformation before you analyze your data. You can choose a data transformation beforehand based on previous data you've collected, or based on the data transformation that others in your field use for your kind of data.

A data transformation will often straighten out a J-shaped curve. If your curve looks U-shaped, S-shaped, or something more complicated, a data transformation won't turn it into a straight line. In that case, you'll have to use curvilinear regression.

Independence. Linear regression and correlation assume that the data points are independent of each other, meaning that the value of one data point does not depend on the value of any other data point. The most common violation of this assumption in regression and correlation is in time series data, where some Y variable has been measured at different times. For example, biologists have counted the number of moose on Isle Royale, a large island in Lake Superior, every year. Moose live a long time, so the number of moose in one year is not independent of the number of moose in the previous year, it is highly dependent on it; if the number of moose in one year is high, the number in the next year will probably be pretty high, and if the number of moose is low one year, the number will probably be low the next year as well. This kind of non-independence, or "autocorrelation," can give you a "significant" regression or correlation much more often than 5% of the time, even when the null hypothesis of no relationship between time and Y is true. If both X and Y are time series—for example, you analyze the number of wolves and the number of moose on Isle Royale—you can also get a "significant" relationship between them much too often.

To illustrate how easy it is to fool yourself with time-series data, I tested the correlation between the number of moose on Isle Royale in the winter and the number of strikeouts thrown by major league baseball teams the following season, using data for 2004–2013. I did this separately for each baseball team, so there were 30 statistical tests. I'm pretty sure the null hypothesis is true (I can't think of anything that would affect both moose abundance in the winter and strikeouts the following summer), so with 30 baseball teams, you'd expect the P value to be less than 0.05 for 5% of the teams, or about one or two. Instead, the P value is significant for 7 teams, which means that if you were stupid enough to test the correlation of moose numbers and strikeouts by your favorite team, you'd have almost a 1-in-4 chance of convincing yourself there was a relationship between the two. Some of the correlations look pretty good: strikeout numbers by the Cleveland team and moose numbers have an r² of 0.70 and a P value of 0.002:

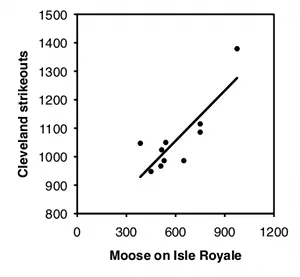Number of moose on Isle Royale and strikeouts by the Cleveland baseball team, showing how easy it is to get an impressive-looking correlation from two autocorrelated data sets.

There are special statistical tests for time-series data. I will not cover them here; if you need to use them, see how other people in your field have analyzed data similar to yours, then find out more about the methods they used.

Spatial autocorrelation is another source of non-independence. This occurs when you measure a variable at locations that are close enough together that nearby locations will tend to have similar values. For example, if you want to know whether the abundance of dandelions is associated with the among of phosphate in the soil, you might mark a bunch of 1 m² squares in a field, count the number of dandelions in each quadrat, and measure the phosphate concentration in the soil of each quadrat. However, both dandelion abundance and phosphate concentration are likely to be spatially autocorrelated; if one quadrat has a lot of dandelions, its neighboring quadrats will also have a lot of dandelions, for reasons that may have nothing to do with phosphate. Similarly, soil composition changes gradually across most areas, so a quadrat with low phosphate will probably be close to other quadrats that are low in phosphate. It would be easy to find a significant correlation between dandelion abundance and phosphate concentration, even if there is no real relationship. If you need to learn about spatial autocorrelation in ecology, Dale and Fortin (2009) is a good place to start.

Another area where spatial autocorrelation is a problem is image analysis. For example, if you label one protein green and another protein red, then look at the amount of red and green protein in different parts of a cell, the high level of autocorrelation between neighboring pixels makes it very easy to find a correlation between the amount of red and green protein, even if there is no true relationship. See McDonald and Dunn (2013) for a solution to this problem.

Examples

A common observation in ecology is that species diversity decreases as you get further from the equator. To see whether this pattern could be seen on a small scale, I used data from the Audubon Society's Christmas Bird Count, in which birders try to count all the birds in a 15-mile diameter area during one winter day. I looked at the total number of species seen in each area on the Delmarva Peninsula during the 2005 count. Latitude and number of bird species are the two measurement variables; location is the hidden nominal variable.

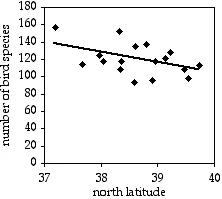Latitude and bird species on the Delmarva Peninsula.

The result is r²=0.214, with 15 d.f., so the P value is 0.061. The trend is in the expected direction, but it is not quite significant. The equation of the regression line is number of species=−12.039×latitude+585.14. Even if it were significant, I don't know what you'd do with the equation; I suppose you could extrapolate and use it to predict that above the 49th parallel, there would be fewer than zero bird species.

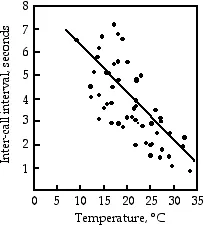Relationship of body temperature and inter-call interval in the gray tree frog.Gray tree frog, Hyla versicolor.

Gayou (1984) measured the intervals between male mating calls in the gray tree frog, Hyla versicolor, at different temperatures. The regression line is interval=−0.205×temperature+8.36, and it is highly significant (r²=0.29, 45 d.f., P=9×10⁻⁵). You could rearrange the equation, temperature=(interval−8.36)/(−0.205), measure the interval between frog mating calls, and estimate the air temperature. Or you could buy a thermometer.

Goheen et al. (2003) captured 14 female northern grasshopper mice (Onchomys leucogaster) in north-central Kansas, measured the body length, and counted the number of offspring. There are two measurement variables, body length and number of offspring, and the authors were interested in whether larger body size causes an increase in the number of offspring, so they did a linear regression. The results are significant: r²=0.46, 12 d.f., P=0.008. The equation of the regression line is offspring=0.108×length−7.88.

Graphing the results

In a spreadsheet, you show the results of a regression on a scatter graph, with the independent variable on the X axis. To add the regression line to the graph, finish making the graph, then select the graph and go to the Chart menu. Choose "Add Trendline" and choose the straight line. If you want to show the regression line extending beyond the observed range of X values, choose "Options" and adjust the "Forecast" numbers until you get the line you want.

Similar tests

Sometimes it is not clear whether an experiment includes one measurement variable and two nominal variables, and should be analyzed with a two-way anova or paired t–test, or includes two measurement variables and one hidden nominal variable, and should be analyzed with correlation and regression. In that case, your choice of test is determined by the biological question you're interested in. For example, let's say you've measured the range of motion of the right shoulder and left shoulder of a bunch of right-handed people. If your question is "Is there an association between the range of motion of people's right and left shoulders—do people with more flexible right shoulders also tend to have more flexible left shoulders?", you'd treat "right shoulder range-of-motion" and "left shoulder range-of-motion" as two different measurement variables, and individual as one hidden nominal variable, and analyze with correlation and regression. If your question is "Is the right shoulder more flexible than the left shoulder?", you'd treat "range of motion" as one measurement variable, "right vs. left" as one nominal variable, individual as one nominal variable, and you'd analyze with two-way anova or a paired t–test.

If the dependent variable is a percentage, such as percentage of people who have heart attacks on different doses of a drug, it's really a nominal variable, not a measurement. Each individual observation is a value of the nominal variable ("heart attack" or "no heart attack"); the percentage is not really a single observation, it's a way of summarizing a bunch of observations. One approach for percentage data is to arcsine transform the percentages and analyze with correlation and linear regression. You'll see this in the literature, and it's not horrible, but it's better to analyze using logistic regression.

If the relationship between the two measurement variables is best described by a curved line, not a straight one, one possibility is to try different transformations on one or both of the variables. The other option is to use curvilinear regression.

If one or both of your variables are ranked variables, not measurement, you should use Spearman rank correlation. Some people recommend Spearman rank correlation when the assumptions of linear regression/correlation (normality and homoscedasticity) are not met, but I'm not aware of any research demonstrating that Spearman is really better in this situation.

To compare the slopes or intercepts of two or more regression lines to each other, use ancova.

If you have more than two measurement variables, use multiple regression.

How to do the test

Spreadsheet

I have put together a spreadsheet to do linear regression and correlation on up to 1000 pairs of observations. It provides the following:

• The regression coefficient (the slope of the regression line).
• The Y intercept. With the slope and the intercept, you have the equation for the regression line: Ŷ=a+bX, where a is the y intercept and b is the slope.
• The r² value.
• The degrees of freedom. There are n−2 degrees of freedom in a regression, where n is the number of observations.
• The P value. This gives you the probability of finding a slope that is as large or larger than the observed slope, under the null hypothesis that the true slope is 0.
• A Y estimator and an X estimator. This enables you to enter a value of X and find the corresponding value of Y on the best-fit line, or vice-versa. This would be useful for constructing standard curves, such as used in protein assays for example.

Web pages

Web pages that will perform linear regression are here, here, and here. They all require you to enter each number individually, and thus are inconvenient for large data sets. This web page does linear regression and lets you paste in a set of numbers, which is more convenient for large data sets.

R

Salvatore Mangiafico's R Companion has a sample R program for correlation and linear regression.

SAS

You can use either PROC GLM or PROC REG for a simple linear regression; since PROC REG is also used for multiple regression, you might as well learn to use it. In the MODEL statement, you give the Y variable first, then the X variable after the equals sign. Here's an example using the bird data from above.

DATA birds;

  INPUT town $ state $ latitude species;

  DATALINES;

Bombay_Hook          DE     39.217     128

Cape_Henlopen        DE     38.800     137

Middletown           DE     39.467     108

Milford              DE     38.958     118

Rehoboth             DE     38.600     135

Seaford-Nanticoke    DE     38.583      94

Wilmington           DE     39.733     113

Crisfield            MD     38.033     118

Denton               MD     38.900      96

Elkton               MD     39.533      98

Lower_Kent_County    MD     39.133     121

Ocean_City           MD     38.317     152

Salisbury            MD     38.333     108

S_Dorchester_County  MD     38.367     118

Cape_Charles         VA     37.200     157

Chincoteague         VA     37.967     125

Wachapreague         VA     37.667     114

;

PROC REG DATA=birds;

  MODEL species=latitude;

  RUN;

The output includes an analysis of variance table. Don't be alarmed by this; if you dig down into the math, regression is just another variety of anova. Below the anova table are the r², slope, intercept, and P value:

Root MSE             16.37357    R-Square     0.2143 r²

Dependent Mean      120.00000    Adj R-Sq     0.1619

Coeff Var            13.64464

                       Parameter Estimates

              Parameter   Standard

Variable   DF   Estimate      Error  t Value  Pr > |t|

              intercept

Intercept   1  585.14462  230.02416     2.54    0.0225

latitude    1  -12.03922    5.95277    -2.02    0.0613 P value

               slope

These results indicate an r² of 0.21, intercept of 585.1, a slope of −12.04, and a P value of 0.061.