Correlation versus linear regression

The statistical tools used for hypothesis testing, describing the closeness of the association, and drawing a line through the points, are correlation and linear regression. Unfortunately, I find the descriptions of correlation and regression in most textbooks to be unnecessarily confusing. Some statistics textbooks have correlation and linear regression in separate chapters, and make it seem as if it is always important to pick one technique or the other. I think this overemphasizes the differences between them. Other books muddle correlation and regression together without really explaining what the difference is.

There are real differences between correlation and linear regression, but fortunately, they usually don't matter. Correlation and linear regression give the exact same P value for the hypothesis test, and for most biological experiments, that's the only really important result. So if you're mainly interested in the P value, you don't need to worry about the difference between correlation and regression.

For the most part, I'll treat correlation and linear regression as different aspects of a single analysis, and you can consider correlation/linear regression to be a single statistical test. Be aware that my approach is probably different from what you'll see elsewhere.

The main difference between correlation and regression is that in correlation, you sample both measurement variables randomly from a population, while in regression you choose the values of the independent (X) variable. For example, let's say you're a forensic anthropologist, interested in the relationship between foot length and body height in humans. If you find a severed foot at a crime scene, you'd like to be able to estimate the height of the person it was severed from. You measure the foot length and body height of a random sample of humans, get a significant P value, and calculate r² to be 0.72. This is a correlation, because you took measurements of both variables on a random sample of people. The r² is therefore a meaningful estimate of the strength of the association between foot length and body height in humans, and you can compare it to other r² values. You might want to see if the r² for feet and height is larger or smaller than the r² for hands and height, for example.

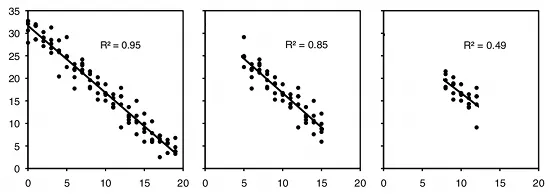
As an example of regression, let's say you've decided forensic anthropology is too disgusting, so now you're interested in the effect of air temperature on running speed in lizards. You put some lizards in a temperature chamber set to 10°C, chase them, and record how fast they run. You do the same for 10 different temperatures, ranging up to 30°C. This is a regression, because you decided which temperatures to use. You'll probably still want to calculate r², just because high values are more impressive. But it's not a very meaningful estimate of anything about lizards. This is because the r² depends on the values of the independent variable that you chose. For the exact same relationship between temperature and running speed, a narrower range of temperatures would give a smaller r². Here are three graphs showing some simulated data, with the same scatter (standard deviation) of Y values at each value of X. As you can see, with a narrower range of X values, the r² gets smaller. If you did another experiment on humidity and running speed in your lizards and got a lower r², you couldn't say that running speed is more strongly associated with temperature than with humidity; if you had chosen a narrower range of temperatures and a broader range of humidities, humidity might have had a larger r² than temperature.

Simulated data showing the effect of the range of X values on the r². For the exact same data, measuring Y over a smaller range of X values yields a smaller r².

If you try to classify every experiment as either regression or correlation, you'll quickly find that there are many experiments that don't clearly fall into one category. For example, let's say that you study air temperature and running speed in lizards. You go out to the desert every Saturday for the eight months of the year that your lizards are active, measure the air temperature, then chase lizards and measure their speed. You haven't deliberately chosen the air temperature, just taken a sample of the natural variation in air temperature, so is it a correlation? But you didn't take a sample of the entire year, just those eight months, and you didn't pick days at random, just Saturdays, so is it a regression?

If you are mainly interested in using the P value for hypothesis testing, to see whether there is a relationship between the two variables, it doesn't matter whether you call the statistical test a regression or correlation. If you are interested in comparing the strength of the relationship (r²) to the strength of other relationships, you are doing a correlation and should design your experiment so that you measure X and Y on a random sample of individuals. If you determine the X values before you do the experiment, you are doing a regression and shouldn't interpret the r² as an estimate of something general about the population you've observed.