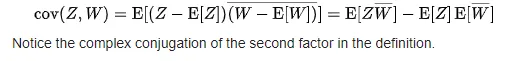Covariance
In probability theory and statistics, covariance is a measure of the joint variability of two random variables.[1] If the greater values of one variable mainly correspond with the greater values of the other variable, and the same holds for the lesser values, (i.e., the variables tend to show similar behavior), the covariance is positive.[2] In the opposite case, when the greater values of one variable mainly correspond to the lesser values of the other, (i.e., the variables tend to show opposite behavior), the covariance is negative. The sign of the covariance therefore shows the tendency in the linear relationship between the variables. The magnitude of the covariance is not easy to interpret because it is not normalized and hence depends on the magnitudes of the variables. The normalized version of the covariance, the correlation coefficient, however, shows by its magnitude the strength of the linear relation.
A distinction must be made between the covariance of two random variables, which is a population parameter that can be seen as a property of the joint probability distribution, and the sample covariance, which in addition to serving as a descriptor of the sample, also serves as an estimated value of the population parameter.
Definition

The covariance between two complex random variables Z,W is defined as