Replacement Theory

Replacement Theory in Operations Research – An Algorithm using MS-Excel

The Replacement Theory in Operations Research is used in the decision making process of replacing a used equipment with a substitute; mostly a new equipment of better usage. The replacement might be necessary due to the deteriorating property or failure or breakdown of particular equipment. The ‘Replacement Theory’ is used in the cases like; existing items have out-lived, or it may not be economical anymore to continue with them, or the items might have been destroyed either by accident or otherwise. The above discussed situations can be solved mathematically and categorised on some basis like:

·         Items that deteriorate with time e.g. machine tools, vehicles, equipment  buildings etc,

·         Items becoming out-of-date due to new developments like ordinary weaving looms by automatic, manual accounting by tally etc.

·         Items which do not deteriorate but fail completely after certain amount of use like electronic parts, street lights etc (Group Replacement) and

·         The existing working staff in an organization gradually diminishing due to death, retirement, retrenchment & otherwise (Staff Replacement).

Replacement Policy for Equipments which Deteriorate Gradually

Let us see the first case of gradual failure of items with time. Consider the example of a Motor Vehicle; the pattern of failure here is progressive in nature i.e. as the life of vehicle increases; its efficiency decreases. This results in additional expenditure in running or maintaining this vehicle and at the same time its resale value (also called as scrap value) also keeps on decreasing. The above case makes this situation a typical case for applying ‘Replacement Theory’.

Example:

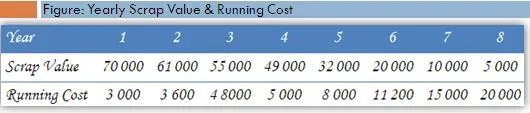
A transport company purchased a motor vehicle for rupees 80000/-. The resale value of the vehicle keeps on decreasing from Rs 70000/- in the first year to Rs 5000/- in the eighth year while, the running cost in maintaining the vehicle keeps on increasing with Rs. 3000/- in the first year till it goes to Rs. 20000/- in the eighth year as shown in the below table. Determine the optimum replacement policy?

The MS-Excel Files of this Algorithm can be downloaded from the links provided further in this post. The cost of the equipment is to be entered in the cell B1 (as shown by the green cell with 80000). Now, enter the scrap values and the running costs as entered in the green columns C5 to C12 and D5 to D12.  The algorithm will now automatically calculate the solution which is as shown in the below figure.

The answer can be fetched from the last column. See the pattern; the average total cost (ATC) at first starts dipping from Rs. 13000/- till it reaches Rs. 11850/- in the cell H8. From H9 it again starts increasing. This cost at which the ATC is lowest in a particular year (after which it starts increasing again) gives the optimum replacement period and cost of the vehicle.

Solution: The vehicle needs to be replaced after four years of its purchase wherein the cost of maintaining that vehicle would be lowest at an average of Rs 11850/- per year.

Clarification on the Methodology

There are two considerations here. First, the running cost (Rn) is increasing every year at the same time the vehicle is depreciating in its value. This depreciation is ‘(C-S)’ i.e. in the first year the scrap value of the vehicle is Rs. 70000/- which was purchased for Rs. 80000/- . So, the vehicle is depreciated by Rs. 10000/- in year one and so on (see column F).

Thus the total cost in keeping this vehicle is this depreciation and its maintenance. The maintenance is made cumulative by adding previous years running cost to it every successive year. Let’s make this simple!

The depreciation is Rs. 10000/- in the first, 19000/- in the second, 25000/- in the third and so on. See here, the vehicle is depreciated by Rs. 25000/- “by” the third year and not “in” the third year. Note that the non-cumulative cost of depreciation “in” the third year would be Rs. 6000/- [Rs. 25000/ minus Rs. 19000/, see the cells F6 and F7]

As, the depreciation in itself is a cumulative function here, we make the running cost cumulative also. That means the cost of maintaining the vehicle “by” the particular years. So, the cost of maintaining the vehicle “by” the third year is Rs. 11400/- (D5+D6+ D7 or 3000+3600+4800).

Hence the total cost incurred by the third year would be Rs. 25000 + Rs. 11400 = Rs. 36400 (see cell G7). Finally, the “average cost” of keeping this vehicle for three years would be 36400 divided by 3 years i.e. Rs. 12133.33 as can be seen from cell H7 and so on.

Notations Used:

·         C –  (Capital) Cost of Equipment

·         S –  Scrap (or Resale) Value

·         Rn –  Running (or Maintenance) Cost

·         E Rn –  Cumulative Running Cost

·         (C-S) –  Depreciation

·         TC –  Total Cost

·         ATC –  Average Total Cost

How to Download?

·         1) Click on the appropriate hyperlinks below

·         Replacement Algorithm (Office 2007 Version)

·         Replacement Algorithm (Office 97-2003 Compatible Version)

·         2) On the sky-blue status bar of ‘Google Docs’; select  “File”

·         3) “Download As” then “Excel”;  [Open with MS Excel (default)? Select  ‘OK’]

·         4) Save the File on your PC and work with it. Happy Solving!!!

Instruction on – How to use the Algorithm Files?

1.      Download the Algorithm file and save it to a location like ‘My Documents’ (This is your Master File)

2.      Create a copy for yourself by using “Save As” command and save the file with a new name maybe into a new location ‘Desktop”

3.      Do not delete the ‘cell values’ at any point of time during the use; rather; over-write the values. The reason being, once you delete or clear the excel sheet, all the formulae used are lost.

Try This Out !

·         Playing with existing Numerical: Start changing the values in the “Rn” and “S” value columns or better if you change the cost of the vehicle only. For example, in the cell B1; use values lesser than or greater than Rs. 80000/- and observe how the solution changes for different purchase costs.

·         To solve a new Numerical: Start overwriting new values for C, S and Rn in the green cells and get the solutions. If say scrap value is not given then you can over-write all the existing scrap values with ‘zeroes’. If the numerical has data gathered for lesser years / periods (in our case the data gathered was for 8 years); then overwrite the remaining values with ‘zeroes’. Do not save the file or if you want to, then use ‘Save As’.