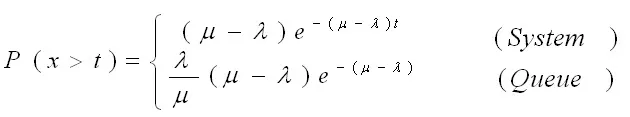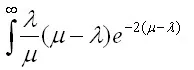
CLASSIFICATION OF QUEUING MODELS AND THEIR SOLUTIONS

Different models in queuing theory are classified by using special (or standard) notations described initially by D.G.Kendall in 1953 in the form (a/b/c). Later A.M.Lee in 1966 added the symbols d and c to the Kendall notation. Now in the literature of queuing theory the standard format used to describe the main characteristics of parallel queues is as follows:

                   {(a/b/c) : (d/c)}

Where

a = arrivals distribution

b = service time (or departures) distribution

c = number of service channels (servers)

d = max. number of customers allowed in the system (in queue plus in service)

e = queue (or service) discipline.

Certain descriptive notations are used for the arrival and service time distribution (i.e. to replace notation a and b) as following:

M = exponential (or markovian) inter-arrival times or service-time distribution (or    equivalently poisson or markovian arrivel or departure distribution)

D = constant or deterministic inter-arrival-time or service-time.

G = service time (departures) distribution of general type, i.e. no assumption is made about the type of distribution.

GI = Inter-arrival time (arrivals) having a general probability distribution such as as normal, uniform or any empirical distribution.

E_k = Erlang-k distribution of inter-arrival or service time distribution with parameter k (i.e. if k= 1, Erlang is equivalent to exponential and if k = , Erlang is equivalent to deterministic).

 For example, a queuing system in which the number of arrivals is described by a Poisson probability distribution, the service time is described by an exponential distribution, and there is a single server, would be designed by M/M/I.

The Kendall notation now will be used to define the class to which a queuing model belongs. The usefulness of a model for a particular situation is limited by its assumptions.

 Model 1 :{( M/M1): (/FCFS)} single server, unlimited queue model

 The derivation of this model is based on certain assumptions about the queuing system:

1.      Exponential distribution of inter-arrival times or poisson distribution of arrival rate.

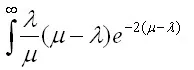
2.      Single waiting line with no restriction on length of queue (i.e. infinite capacity) and no banking or reneging.

3.      Queue discipline is ‘first-come, first-serve

4.      Single serve with exponential distribution of service time

Performance characteristics

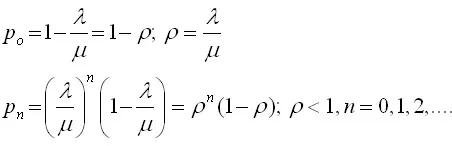
       P_w   = probability of server being busy (i.e. customer has to wait) =  1-Ρ_{o= λ / µ}

1.Expected (or average) number of customer in the system (customers in the line plus the customer being served)

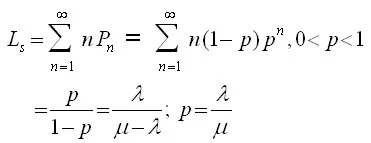
2.Expected (or average) queue length or expected number of customers waiting in the queue

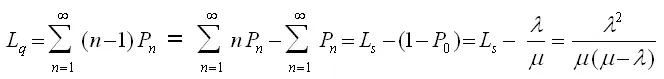
3.Expected (or average) waiting time of a customer in the queue

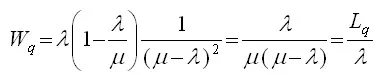
4.Expected (or average) waiting time of a customer in the system (waiting and service)

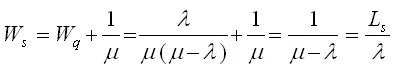
5.Expected (or average) waiting time in the queue for busy system

6.Probability of k or more customers in the system

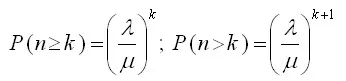
7.The variance (fluctuation) of queue length

 Var (n) =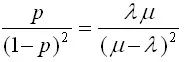 

8.Expected non-empty queue length

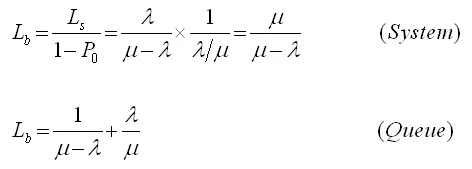
9.Probability that waiting time is more than