Requirement of Linear Programme Problem (L.P.P) | Operations Research
After reading this article you will learn about the requirement of Linear Programme Problem (L.P.P).
Linear programming is an optimization technique for finding an optimal (maximum or minimum) value of a function, called objective function, of several independent variables, the variable being subject to various restrictions expressed as equation or inequalities.
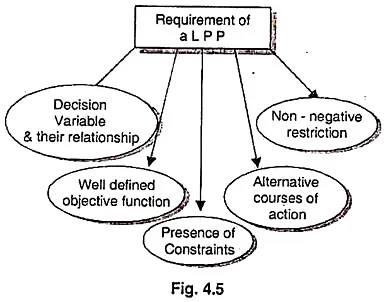
The term linear indicates that the function to be maximized or minimized is linear in nature and that the corresponding constraints be represented by a system of linear equalities or linear equation involving the variable. Regardless of the way one defines linear programming, certain basic requirements which are given below are necessary before the technique can be employed for optimization problems.
The decision variables refer to candidates that are completing with one another for sharing the given limited resources. These variables are usually interrelated in terms of utilization of resources and need simultaneous solutions. The relationship among these variables should be linear.
A linear programming problem must have a clearly- defined objective function to optimize which may be either to maximize contribution by utilizing available resources, or it may be to produce at the lowest possible cost by using a limited amount of productive factors. It should be expressed as a linear function of decision variables and can be represented in the following form.
Optimize (maximize or minimize) z = C1x1 + C2x2 +……………… + Cnxn
Where Z is the measure-of-performance variable. Which is a function of x1, x2, ……xn.
The C1, C2……….. C4 are parameters that give the contribution of a unit of the respective Variable x1, x2, ………………… xn to the measure-of-performance Z.
There must be limitations or constraints on the use of limited resources which are to be allocated among various competitive activities. These constraints must be capable of being expressed as linear equalities or inequalities in terms of decision variables. The solution of on LP model satisfy these constraints.
There must be alternative courses of action. For example, it must be possible to make a selection between various combinations of the productive factors such as men, machines, materials, market-etc.
All decision variables must assume non-negative values as negative values of physical quantities is an impossible situation.
In other words, x1 ≥ 0; x2 ≥ 0……….. xn ≥ 0