What is Linear Programming?

Now, what is linear programming? Linear programming is a simple technique where we depict complex relationships through linear functions and then find the optimum points. The important word in previous sentence is depict. The real relationships might be much more complex – but we can simplify them to linear relationships.

Applications of linear programming are every where around you. You use linear programming at personal and professional fronts. You are using linear programming when you are driving from home to work and want to take the shortest route. Or when you have a project delivery you make strategies to make your team work efficiently for on time delivery.

Example of a linear programming problem

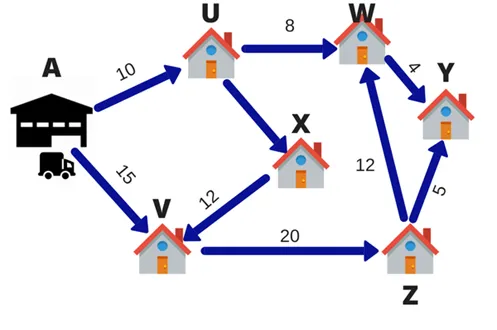
Let’s say a FedEx delivery man has 6 packages to deliver in a day. The warehouse is located at point A. The 6 delivery destinations are given by U, V, W, X, Y and Z. The numbers on the lines indicate the distance between the cities. To save on fuel and time the delivery person wants to take the shortest route.

So, the delivery person will calculate different routes for going to all the 6 destinations and then come up with the shortest route. This technique of choosing the shortest route is called linear programming.

In this case, the objective of the delivery person is to deliver the parcel on time at all 6 destinations. The process of choosing the best route is called Operation Research. Operation research is an approach to decision-making, which involves a set of methods to operate a system. In the above example, my system was the Delivery model.

Linear programming is used for obtaining the most optimal solution for a problem with given constraints. In linear programming, we formulate our real life problem into a mathematical model. It involves an objective function, linear inequalities with subject to constraints.

Is the linear representation of the 6 points above representative of real world? Yes and No. It is oversimplification as the real route would not be a straight line. It would likely have multiple turns, U turns, signals and traffic jams. But with a simple assumption, we have reduced the complexity of the problem drastically and are creating a solution which should work in most scenarios.

 Formulating a problem – Let’s manufacture some chocolates

Example: Consider a chocolate manufacturing company which produces only two types of chocolate – A and B. Both the chocolates require Milk and Choco only.  To manufacture each unit of A and B, following quantities are required:

• Each unit of A requires 1 unit of Milk and 3 units of Choco
• Each unit of B requires 1 unit of Milk and 2 units of Choco

The company kitchen has a total of 5 units of Milk and 12 units of Choco. On each sale, the company makes a profit of

• Rs 6 per unit A sold
• Rs 5 per unit B sold.

Now, the company wishes to maximize its profit. How many units of A and B should it produce respectively?

Solution: The first thing I’m gonna do is represent the problem in a tabular form for better understanding.

Let the total number of units produced of A be = X

Let the total number of units produced of B be = Y

Now, the total profit is represented by Z

The total profit the company makes is given by the total number of units of A and B produced multiplied by its per unit profit Rs 6 and Rs 5 respectively.

Profit: Max Z = 6X+5Y

which means we have to maximize Z.

The company will try to produce as many units of A and B to maximize the profit. But the resources Milk and Choco are available in limited amount.

As per the above table, each unit of A and B requires 1 unit of Milk. The total amount of Milk available is 5 units. To represent this mathematically,

X+Y ≤ 5

Also, each unit of A and B requires 3 units & 2 units of Choco respectively. The total amount of Choco available is 12 units. To represent this mathematically,

3X+2Y ≤ 12

Also, the values for units of A can only be integers.

So we have two more constraints, X ≥ 0  &  Y ≥ 0

For the company to make maximum profit, the above inequalities have to be satisfied.

This is called formulating a real-world problem into a mathematical model.

 Common terminologies used in Linear Programming

Let us define some terminologies used in Linear Programming using the above example.

• Decision Variables: The decision variables are the variables which will decide my output. They represent my ultimate solution. To solve any problem, we first need to identify the decision variables. For the above example, the total number of units for A and B denoted by X & Y respectively are my decision variables.
• Objective Function: It is defined as the objective of making decisions. In the above example, the company wishes to increase the total profit represented by Z. So, profit is my objective function.
• Constraints: The constraints are the restrictions or limitations on the decision variables. They usually limit the value of the decision variables. In the above example, the limit on the availability of resources Milk and Choco are my constraints.
• Non-negativity restriction: For all linear programs, the decision variables should always take non-negative values. Which means the values for decision variables should be greater than or equal to 0.

Process to formulate a Linear Programming problem

Let us look at the steps of defining a Linear Programming problem generically:

1. Identify the decision variables
2. Write the objective function
3. Mention the constraints
4. Explicitly state the non-negativity restriction

For a problem to be a linear programming problem, the decision variables, objective function and constraints all have to be linear functions.

If the all the three conditions are satisfied, it is called a Linear Programming Problem.