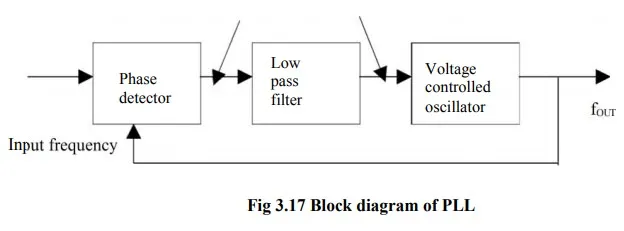
Operation of Basic Phase Locked Loop
Operation of Basic Phase Locked Loop

The PLL consists of i) Phase detector ii) LPF iii) VCO. The phase detector or comparator compares the input frequency fIN with feedback frequency fOUT.
· The output of the phase detector is proportional to the phase difference between fIN & fOUT. The output of the phase detector is a dc voltage & therefore is often referred to as the error voltage.
· The output of the phase detector is then applied to the LPF, which removes the high frequency noise and produces a dc level. This dc level in turn, is input to the VCO.
· The output frequency of VCO is directly proportional to the dc level. The VCO frequency is compared with input frequency and adjusted until it is equal to the input frequencies.
· PLL goes through 3 states, i) free running ii) Capture iii) Phase lock.
Before the input is applied, the PLL is in free running state. Once the input frequency is applied the VCO frequency starts to change and PLL is said to be in the capture mode. The VCO frequency continuous to change until it equals the input frequency and the PLL is in phase lock mode. When Phase locked, the loop tracks any change in the input frequency through its repetitive action.
If an input signal vs of frequency fs is applied to the PLL, the phase detector compares the phase and frequency of the incoming signal to that of the output vo of the VCO. If the two signals differ in frequency of the incoming signal to that of the output vo of the VCO.
The phase detector is basically a multiplier and produces the sum (fs + fo) and difference (fs - fo) components at its output.
The high frequency component (fs + fo) is removed by the low pass filter and the difference frequency component is amplified then applied as control voltage vc to VCO.
The signal vc shifts the VCO frequency in a direction to reduce the frequency difference between fs and fo. Once this action starts, we say that the signal is in the capture range. The VCO continues to change frequency till its output frequency is exactly the same as the input signal frequency. The circuit is then said to be locked. Once locked, the output frequency fo of VCO is identical to fs except for a finite phase difference φ. This phase difference φ generates a corrective control voltage vc to shift the VCO frequency from f0 to fs and thereby maintain the lock. Once locked, PLL tracks the frequency changes of the input signal. Thus, a PLL goes through three stages (i) free running, (ii) capture and (iii) locked or tracking.
Capture range: the range of frequencies over which the PLL can acquire lock with an input signal is called the capture range. This parameter is also expressed as percentage of fo.
Pull-in time: the total time taken by the PLL to establish lock is called pull-in time. This depends on the initial phase and frequency difference between the two signals as well as on the overall loop gain and loop filter characteristics.
Phase Detector
Phase detector compares the input frequency and VCO frequency and generates DC voltage i.e., proportional to the phase difference between the two frequencies. Depending on whether the analog/digital phase detector is used, the PLL is called either an analog/digital type respectively. Even though most monolithic PLL integrated circuits use analog phase detectors.
Ex for Analog: Double-balanced mixer
Ex for Digital: Ex-OR, Edge trigger, monolithic Phase detector.
Ex-OR Phase Detector:
This uses an exclusive OR gate. The output of the Ex-OR gate is high only when fIN or fOUT is high.
The DC output voltage of the Ex-OR phase detector is a function of the phase difference between its two outputs. The maximum dc output voltage occurs when the phase difference is Π radians or
180 degrees. The slope of the curve between 0 or Π radians is the conversion gain kp of the phase detector for eg; if the Ex-OR gate uses a supply voltage Vcc = 5V, the conversion gain Kp is
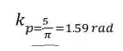
Advantages of Edge Triggered Phase Detector over Ex-OR are
i) The dc output voltage is linear over 2Π radians or 360 degrees, but in Ex-OR it is Π radians or 180 degrees.
ii) Better Capture, tracking & locking characteristics.
Edge triggered type of phase detector using RS Flip – Flop. It is formed from a pair of cross coupled NOR gates.
RS FF is triggered, i.e., the output of the detector changes its logic state on the positive edge of the inputs fIN & fOUT
• It consists of 2 digital phase detector, a charge pump and an amplifier.
• Phase detector 1 is used in applications that require zero frequency and phase difference at lock.
• Phase detector 2, if quadrature lock is desired, when detector 1 is used in the main loop, detector can also be used to indicate whether the main loop is in lock or out of lock.
Low – Pass filter
The function of the LPF is to remove the high frequency components in the output of the phase detector and to remove the high frequency noise. LPF controls the characteristics of the phase locked loop. i.e., capture range, lock ranges, bandwidth
· Lock range(Tracking range):
The lock range is defined as the range of frequencies over which the PLL system follows the changes in the input frequency fIN.
· Capture range:
Capture range is the frequency range in which the PLL acquires phase lock. Capture range is always smaller than the lock range.
· Filter Bandwidth:
Filter Bandwidth is reduced, its response time increases. However reduced Bandwidth reduces the capture range of the PLL. Reduced Bandwidth helps to keep the loop in lock through momentary losses of signal and also minimizes noise.
Voltage Controlled Oscillator (VCO):
The third section of PLL is the VCO; it generates an output frequency that is directly proportional to its input voltage. The maximum output frequency of NE/SE 566 is 500 Khz.
Feedback path and optional divider:
Most PLLs also include a divider between the oscillator and the feedback input to the phase detector to produce a frequency synthesizer. A programmable divider is particularly useful in radio Transmitter applications, since a large number of transmit frequencies can be produced from a single stable, accurate, but expensive, quartz crystal–controlled reference oscillator.
Some PLLs also include a divider between the reference clock and the reference input to the phase detector. If this divider divides by M, it allows the VCO to multiply the reference frequency by N / M. It might seem simpler to just feed the PLL a lower frequency, but in some cases the reference frequency may be constrained by other issues, and then the reference divider is useful.
Frequency multiplication in a sense can also be attained by locking the PLL to the 'N'th harmonic of the signal.
The equations governing a phase-locked loop with an analog multiplier as the phase detector may be derived as follows. Let the input to the phase detector be xc(t) and the output of the voltage- controlled oscillator (VCO) is xr(t) with frequency ωr(t), then the output of the phase detector xm(t) is given by
xm(t) = xc(t) + xr(t)
the VCO frequency may be written as a function of the VCO input y(t) as
ωr(t) = ωf + gvy(t)
where gv is the sensitivity of the VCO and is expressed in Hz / V.
Hence the VCO output takes the form
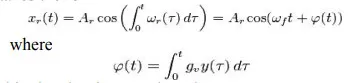
The loop filter receives this signal as input and produces an
output xf(t) = Ffilter(xm(t))
where Filter is the operator representing the loop filter transformation.
When the loop is closed, the output from the loop filter becomes the input to the VCO thus
y(t) = xf(t) = Ffilter(xm(t))
We can deduce how the PLL reacts to a sinusoidal input signal:
xc(t) = Acsin(ωct).
The output of the phase detector then is:
ωm(t) = Acsin(ωct) Arcos(ωft +φ(t))
This can be rewritten into sum and difference components using trigonometric identities:
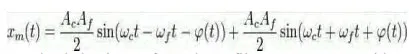
As an approximation to the behaviour of the loop filter we may consider only the difference frequency being passed with no phase change, which enables us to derive a small-signal model of the phase-locked loop. If we can make ωf≈ ωc then the sin (.)can be approximated by its argument resulting in: y(t)=xf(t)=-AcAfφ(t)/ωdt. The phase-locked loop is said to be locked if this is the case.