What is Parity Bit?
The parity generating technique is one of the most widely used error detection techniques for the data transmission. In digital systems, when binary data is transmitted and processed , data may be subjected to noise so that such noise can alter 0s (of data bits) to 1s and 1s to 0s.
Hence, parity bit is added to the word containing data in order to make number of 1s either even or odd.Thus it is used to detect errors , during the transmission of binary data .The message containing the data bits along with parity bit is transmitted from transmitter node to receiver node. At the receiving end, the number of 1s in the message is counted and if it doesn’t match with the transmitted one, then it means there is an error in the data.
A parity generator is a combinational logic circuit that generates the parity bit in the transmitter. On the other hand, a circuit that checks the parity in the receiver is called parity checker. A combined circuit or devices of parity generators and parity checkers are commonly used in digital systems to detect the single bit errors in the transmitted data word.
The sum of the data bits and parity bits can be even or odd . In even parity, the added parity bit will make the total number of 1s an even amount whereas in odd parity the added parity bit will make the total number of 1s odd amount.
The basic principle involved in the implementation of parity circuits is that sum of odd number of 1s is always 1 and sum of even number of 1s is always zero. Such error detecting and correction can be implemented by using Ex-OR gates (since Ex-OR gate produce zero output when there are even number of inputs).
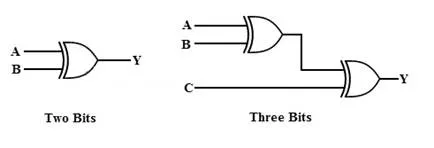
To produce two bits sum, one Ex-OR gate is sufficient whereas for adding three bits two Ex-OR gates are required as shown in below figure.
It is combinational circuit that accepts an n-1 bit stream data and generates the additional bit that is to be transmitted with the bit stream. This additional or extra bit is termed as a parity bit.
In even parity bit scheme, the parity bit is ‘0’ if there are even number of 1s in the data stream and the parity bit is ‘1’ if there are odd number of 1s in the data stream.
In odd parity bit scheme, the parity bit is ‘1’ if there are even number of 1s in the data stream and the parity bit is ‘0’ if there are odd number of 1s in the data stream. Let us discuss both even and odd parity generators.
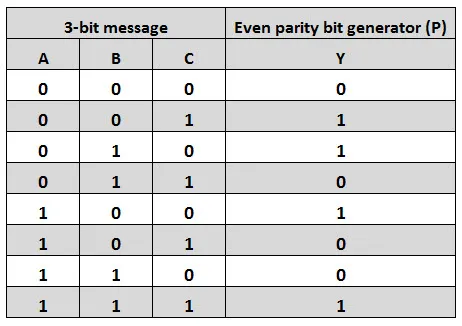
Let us assume that a 3-bit message is to be transmitted with an even parity bit. Let the three inputs A, B and C are applied to the circuits and output bit is the parity bit P. The total number of 1s must be even, to generate the even parity bit P.
The figure below shows the truth table of even parity generator in which 1 is placed as parity bit in order to make all 1s as even when the number of 1s in the truth table is odd.
The K-map simplification for 3-bit message even parity generator is
From the above truth table, the simplified expression of the parity bit can be written as

The above expression can be implemented by using two Ex-OR gates. The logic diagram of even parity generator with two Ex – OR gates is shown below. The three bit message along with the parity generated by this circuit which is transmitted to the receiving end where parity checker circuit checks whether any error is present or not.
To generate the even parity bit for a 4-bit data, three Ex-OR gates are required to add the 4-bits and their sum will be the parity bit.
Let us consider that the 3-bit data is to be transmitted with an odd parity bit. The three inputs are A, B and C and P is the output parity bit. The total number of bits must be odd in order to generate the odd parity bit.
In the given truth table below, 1 is placed in the parity bit in order to make the total number of bits odd when the total number of 1s in the truth table is even.
The truth table of the odd parity generator can be simplified by using K-map as
The output parity bit expression for this generator circuit is obtained as
P = A ⊕ B Ex-NOR C
The above Boolean expression can be implemented by using one Ex-OR gate and one Ex-NOR gate in order to design a 3-bit odd parity generator.
The logic circuit of this generator is shown in below figure , in which . two inputs are applied at one Ex-OR gate, and this Ex-OR output and third input is applied to the Ex-NOR gate , to produce the odd parity bit. It is also possible to design this circuit by using two Ex-OR gates and one NOT gate.