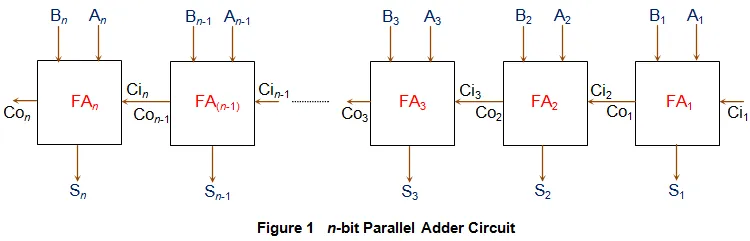
Such a n-bit adder formed by cascading n full adders (FA1 to FAn) is as shown by Figure 1 and is used to add two n-bit binary numbers
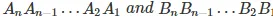 .
.
Parallel Adder
Adders are the combinatorial circuits which are used to add two binary numbers. The nature of the adders chosen depends on the characteristics of the binary numbers which need to be added. Say for example, if one needs to add two single bit binary digits, then one can use half adder while if there is an additional carry which needs to be added along with them, then one may resort to the use of full adder. However what if we want to add a binary number which has multiple bits in it. In such a case, the need arises to use a parallel adder.
Parallel adder is nothing but a cascade of several full adders. The number of full adders used will depend on the number of bits in the binary digits which require to be added.
Such a n-bit adder formed by cascading n full adders (FA1 to FAn) is as shown by Figure 1 and is used to add two n-bit binary numbers 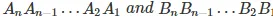 .
.
Here, every single bit of the numbers to be added is provided at the input pins of every single full adder. That is, the first bits A1 and B1 are provided as the inputs to full adder (FA1), the second bits A2 and B2 to the inputs of full adder 2 (FA2)… and the last bits An and Bn to the nth full adder FAn. Next, the carry out pin of each full adder in the circuit is connected to the carry in pin of its succeeding full adder (except in the case of last full adder). For example, the carry out pin of FA1 (Co1) is connected to carry in pin of FA2 (Ci2), the carry out pin of FA2 (Co2) is connected to carry in pin of FA3 (Ci3) and so on and so forth.
In the circuit shown by Figure 1, first, FA1 adds A1 with B1 to generate S1 (the first bit of sum output) and Co1. Next, FA2 uses this Co1 as its carry in bit and adds it with its input bits A2 and B2 to generate the second bit of the sum output S2 and Co2. Next, this Co2 is considered as an input by FA3 which adds it with the bits A3 and B3. This process continues till the nth full adder in the sequence which adds the carry out bit of (n-1)th full adder (Con-1) with its inputs An and Bn. When this happens, we would get the output bits Sn and Con which are the last bits of our sum output and the expected carry bit, respectively.
From the discussion presented we can say that in the case of n-bit parallel adder, each adder has to wait for the carry term to be generated from its preceding adder in order to finish its task of adding. This can be visualized as if the carry term propagates along the chain in the fashion of a ripple. Thus these kind of adders are even referred to as ripple carry adders.
Further, the delay associated with the travelling of carry bit is called carry propagation delay and is found to worsen with an increase in the length of the binary numbers which require to be added. For example, if each full adder is considered to have a delay of 10 ns, then the total delay required to produce the output of a 4-bit parallel adder would be 4 × 10 = 40 ns.