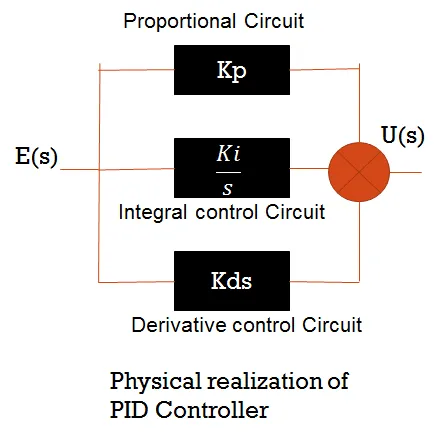
Physical Realisation of PID Controller

Why do You Need a PID Controller

The Characteristics of P, I, and D controllers are briefly discussed With MATLAB Code to give an insight about individual P,PI,PD,PID Controllers

A proportional controller (Kp) will have the effect of reducing the rise time and will reduce, but never eliminate, the steady-state error.
An integral control (Ki) will have the effect of eliminating the steady-state error, but it may make the transient response worse.
A derivative control (Kd) will have the effect of increasing the stability of the system, reducing the overshoot, and improving the transient response but little effect on rise time
A PD Controller could add damping to a system, but the steady-state response is not affected.(steady state error is not eliminated)
A PI Controller could improve relative stability and eliminate steady state error at the same time, but the settling time is increased(System response sluggish)

But a PID controller removes steady-state error and decreases system settling times while maintaining a reasonable transient response

Example::Illustrating P, PI, PD & PID controller in MATLAB

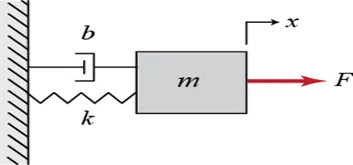
For the Given Spring-Mass-Damper System

Using D’Alembert’s Principle

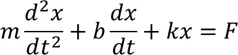
Taking Laplace Transform with Zero initial conditions to get:

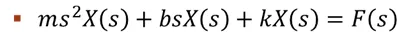
The transfer function between Output X(s) & input F(s) is

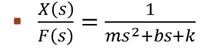
Assuming m=1kg,b=10 Ns/m & k=20 N/m [For Simpicity]

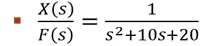
Which is the open loop transfer function

On Matlab Command window, typing following commands, yield Step Response of the system

G=tf(1,[1 10 20]);

Step(G);

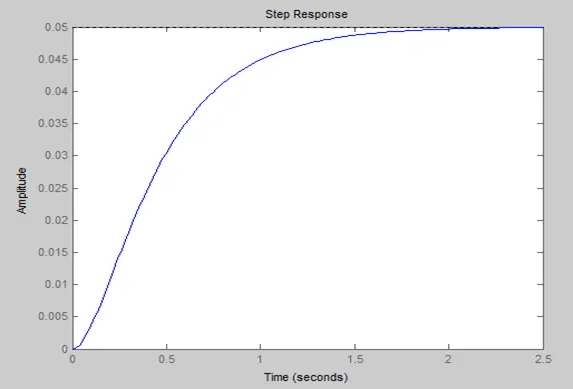
The DC gain of the plant transfer function is 1/20, so 0.05 is the final value of the output to a unit step input. This corresponds to the steady-state error of 0.95, quite large indeed.

Furthermore, the rise time is about one second, and the settling time is about 1.5 seconds.

#Proportional Control

In Proportional control, the actuating signal for the control action in a control system is proportional to the error signal. The error signal being the difference between the reference input signal and the feedback signal obtained from the output

The Transfer function of the controller is:

U(s) = Kp E(s) or, C(s) =Kp

The closed-loop transfer function of the Spring-Mass system with a proportional controller is:

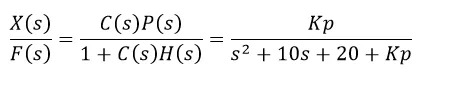
For K_p=500

Executing following Commands in MATLAB will give output on command window

Kp = 500;

C = pid(Kp)

P=tf(1,[1 10 20])

T = feedback(C*P,1)

t = 0:0.01:2;

step (T,t);

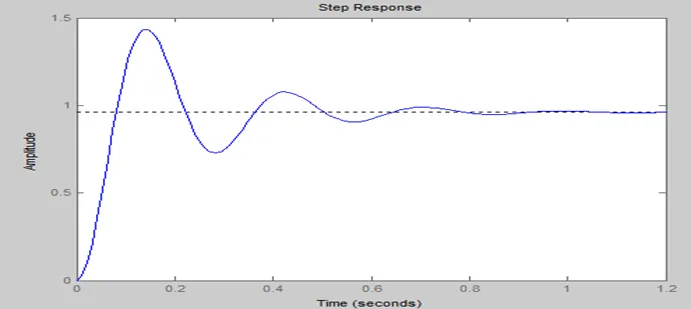
The Step response of the system in MATLAB indicates that the proportional controller (Kp) reduces the rise time, increases the overshoot, reduces the steady state error but never eliminates it completely

This is a type-zero system and hence will have a finite steady-state error for a step input.

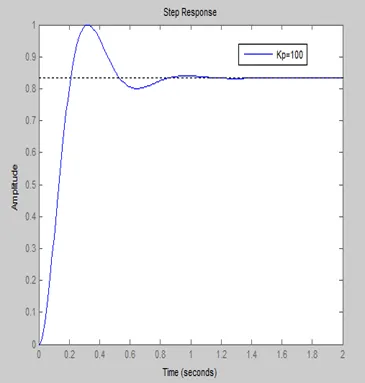
Large values of K lead to small steady-state error; however, they also lead to a faster, less damped responses.

If we want a small overshoot and a small steady-state error, a proportional gain alone is not enough.

#PD Controller

For Derivative control action the actuating signal consists of proportional error signal added with derivative of the error signal

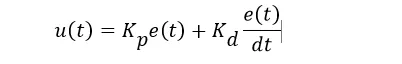
A proportional plus derivative (PD) controller has the transfer function:

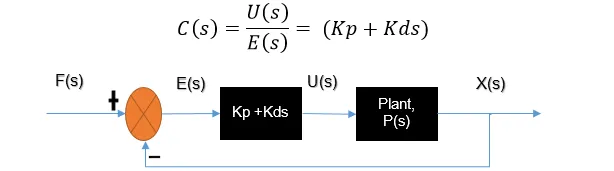
Proportional-derivative (PD) control considers both the magnitude of the system error and the derivative of this error. Derivative control has the effect of adding damping to a system, and, thus, has a stabilizing influence on the system response.

The closed-loop transfer function of

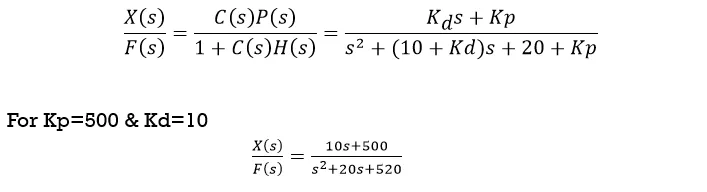
the above system with a PD controller is:

MATLAB Code for PD Controller(Without Tuning Sample Values)

Entering Following commands in MATLAB yields

Kp = 500;

Kd=10;

C = pid(Kp,0,Kd);

P=tf(1,[1 10 20]);

T = feedback(C*P,1)

step(T);

Continuous-time PD controller in parallel form:

Kp + Kd * s

With Kp = 500, Kd = 10

Transfer function:

10 s + 500

—————-

s^2 + 20 s + 520

Without integral control, this is a type-zero system, and hence will have a finite steady state error to a unit step input

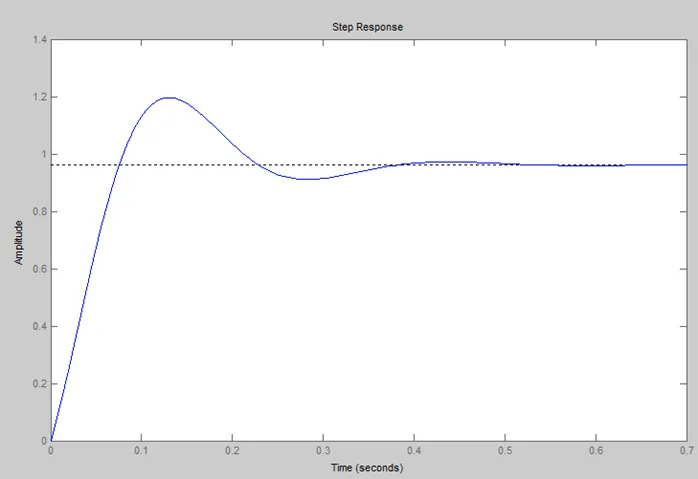
The derivative controller reduced both the overshoot and the Settling time, and had a small effect on the rise time and the steady-state error.

The PD controller has decreased the system settling time considerably; however, to control the steady-state error, the derivative gain Kd must be high. This decreases the response times of the system and can make it susceptible to noise.

Effects of PD Controller :-

Improves damping and maximum overshoot.
Reduces rise time & settling time.
Increases Bandwidth
Improves Gain Margin and Phase Margin
May attenuate high frequency noise

#PI Controller

For Integral control action, the actuating signal consists of proportional-error signal added with integral of the error signal.

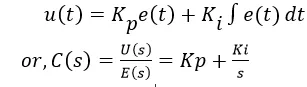
Proportional-integral (PI) control considers both the magnitude of the system error signal and the integral of this error

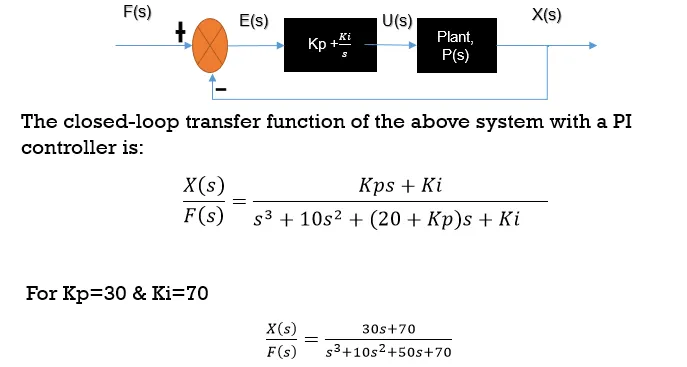
MATLAB Code for PI Controller(Without Tuning Sample Values)

Executing Following commands in MATLAB

Kp = 30;

Ki=70;

C = pid(Kp,Ki)

P=tf(1,[1 10 20]);

T = feedback(C*P,1)

step(T);

Continuous-time PI controller in parallel form:

Kp + Ki * —

With Kp = 30, Ki = 70

Transfer function:

30 s + 70

————————

s^3 + 10 s^2 + 50 s + 70

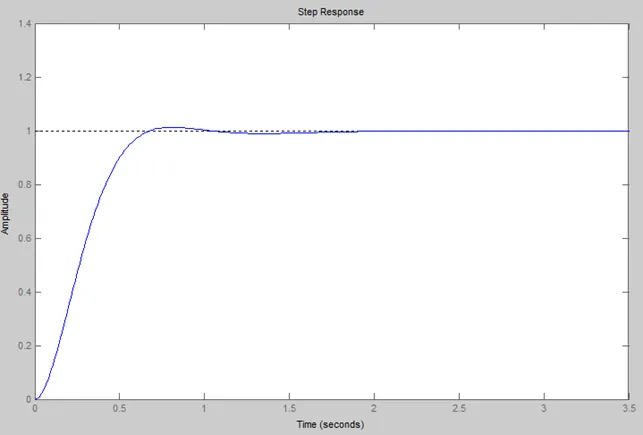
Using integral control makes the system type-one, so the steady-state error due to a step input is zero.

The response shows that the Integral control has removed the steady-state error and improved the transient response, but it has also increased the system settling time.

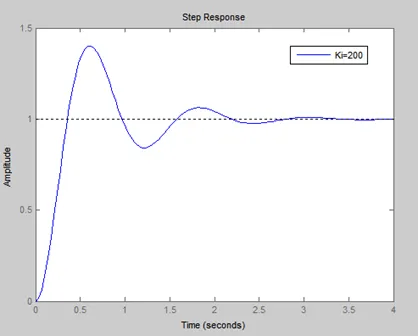
Increasing Ki increases overshoot & settling time making system response sluggish

To reduce both settling time and overshoot, a PI controller by itself is not enough

Effects of PI Controller :-

Improves damping and reduces maximum overshoot.
Increases Rise Time.
Decreases Bandwidth
Improves Gain Margin, Phase margin & Peak Resonance (Mr).
Filter out high frequency noise.