Satellite Orbits and Energy
The Moon orbits Earth. In turn, Earth and the other planets orbit the Sun. The space directly above our atmosphere is filled with artificial satellites in orbit. We examine the simplest of these orbits, the circular orbit, to understand the relationship between the speed and period of planets and satellites in relation to their positions and the bodies that they orbit.
As noted at the beginning of this chapter, Nicolaus Copernicus first suggested that Earth and all other planets orbit the Sun in circles. He further noted that orbital periods increased with distance from the Sun. Later analysis by Kepler showed that these orbits are actually ellipses, but the orbits of most planets in the solar system are nearly circular. Earth’s orbital distance from the Sun varies a mere 2%. The exception is the eccentric orbit of Mercury, whose orbital distance varies nearly 40%.
Determining the orbital speed and orbital period of a satellite is much easier for circular orbits, so we make that assumption in the derivation that follows. As we described in the previous section, an object with negative total energy is gravitationally bound and therefore is in orbit. Our computation for the special case of circular orbits will confirm this. We focus on objects orbiting Earth, but our results can be generalized for other cases.
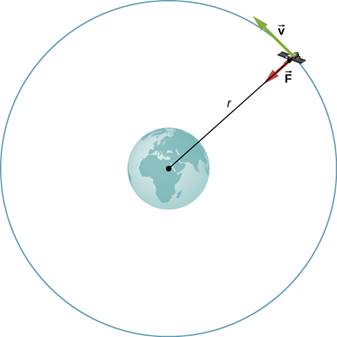
Consider a satellite of mass m in a circular orbit about Earth at distance r from the center of Earth ((Figure)). It has centripetal acceleration directed toward the center of Earth. Earth’s gravity is the only force acting, so Newton’s second law gives
GmMEr2=mac=mv2orbitr.GmMEr2=mac=mvorbit2r.

Figure 13.12 A satellite of mass m orbiting at radius r from the center of Earth. The gravitational force supplies the centripetal acceleration.
We solve for the speed of the orbit, noting that m cancels, to get the orbital speed

.
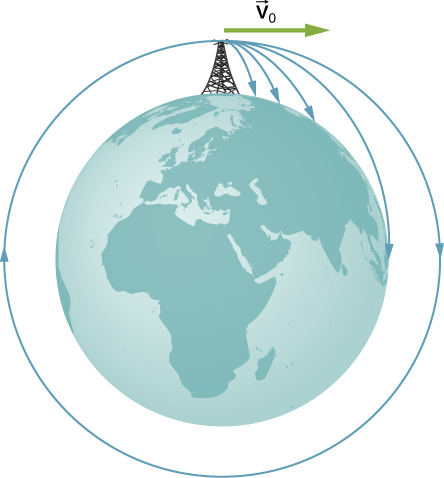
Figure 13.13 A circular orbit is the result of choosing a tangential velocity such that Earth’s surface curves away at the same rate as the object falls toward Earth.
We can summarize our discussion of orbiting satellites in the following Problem-Solving Strategy.
1. Determine whether the equations for speed, energy, or period are valid for the problem at hand. If not, start with the first principles we used to derive those equations.
2. To start from first principles, draw a free-body diagram and apply Newton’s law of gravitation and Newton’s second law.
3. Along with the definitions for speed and energy, apply Newton’s second law of motion to the bodies of interest.
