Optimization

Game trees are, in general, very time consuming to build, and it’s only for simple games that it can be generated in a short time. If there are b legal moves, i.e., b nodes at each point and the maximum depth of the tree is m, the time complexity of the minimax algorithm is of the order bm(O(bm)).

To curb this situation, there are a few optimizations that can be added to the algorithm. Fortunately, it is viable to find the actual minimax decision without even looking at every node of the game tree. Hence, we eliminate nodes from the tree without analyzing, and this process is called pruning.

Alpha-beta pruning

The method that we are going to look in this article is called alpha-beta pruning. If we apply alpha-beta pruning to a standard minimax algorithm, it returns the same move as the standard one, but it removes (prunes) all the nodes that are possibly not affecting the final decision.

Let us understand the intuition behind this first and then we will formalize the algorithm. Suppose, we have the following game tree:

In this case,
Minimax Decision = MAX{MIN{3,5,10}, MIN{2,a,b}, MIN{2,7,3}}
= MAX{3,c,2}
= 3

You would be surprised! How could we calculate the maximum with a missing value? Here is the trick. MIN{2,a,b} would certainly be less than or equal to 2, i.e., c<=2 and hence MAX{3,c,2} has to be 3. The question now is do we really need to calculate c? Of course not. We could have reached to the conclusion without looking at those nodes. And this is where alpha-beta pruning comes into the picture.

A few definitions:

Alpha: It is the best choice so far for the player MAX. We want to get the highest possible value here.
Beta: It is the best choice so far for MIN, and it has to be the lowest possible value.

Note: Each node has to keep track of its alpha and beta values. Alpha can be updated only when it’s MAX’s turn and, similarly, beta can be updated only when it’s MIN’s chance.

How does alpha-beta pruning work?

1. Initialize alpha = -infinity and beta = infinity as the worst possible cases. The condition to prune a node is when alpha becomes greater than or equal to beta.
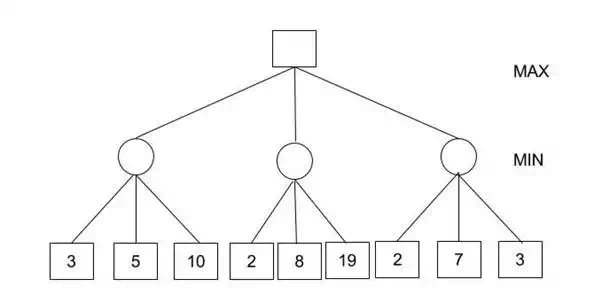
2. Start with assigning the initial values of alpha and beta to root and since alpha is less than beta we don’t prune it.
3. Carry these values of alpha and beta to the child node on the left. And now from the utility value of the terminal state, we will update the values of alpha and be, so we don’t have to update the value of beta. Again, we don’t prune because the condition remains the same. Similarly, for the third child node also. And then backtracking to the root we set alpha=3 because that is the minimum value that alpha can have.
   
4. Now, alpha=3 and beta=infinity at the root. So, we don’t prune. Carrying this to the center node, and calculating MIN{2, infinity}, we get alpha=3 and beta=2.
5. Prune the second and third child nodes because alpha is now greater than beta.
6. Alpha at the root remains 3 because it is greater than 2. Carrying this to the rightmost child node, evaluate MIN{infinity,2}=2. Update beta to 2 and alpha remains 3.
7. Prune the second and third child nodes because alpha is now greater than beta.
8. Hence, we get 3, 2, 2 at the left, center, and right MIN nodes, respectively. And calculating MAX{3,2,2}, we get 3. Therefore, without even looking at four leaves we could correctly find the minimax decision.