Truth Tables

· We can use variables to represent possible truth values, in much the same way that variables are used in algebra to represent possible numerical values.

· We can then apply logical operators to these variables and can reason about the way in which they behave.

· It is usual to represent the behavior of these logical operators using truth tables.

· A truth table shows the possible values that can be generated by applying an operator to truth values.

Not

· First of all, we will look at the truth table for not, ￢.

· Not is a unary operator, which means it is applied only to one variable.

· Its behavior is very simple:

§ true is equal to false

§ false is equal to true

If variable A has value true, then ￢A has value false.

If variable B has value false, then ￢B has value true.

And

· Now, let us examine the truth table for our first binary operator—one which acts on two variables:

· ∧is also called the conjunctive operator.

· A ∧B is the conjunction of A and B.

· You can see that the only entry in the truth table for which A ∧B is true is the one where A is true and B is true. If A is false, or if B is false, then A ∧B is false. If both A and B are false, then A ∧B is also false.

· What do A and B mean? They can represent any statement, or proposition, that can take on a truth value.

· For example, A might represent “It’s sunny,” and B might represent “It’s warm outside.” In this case, A ∧ B would mean “It is sunny and it’s warm outside,” which clearly is true only if the two component parts are true (i.e., if it is true that it is sunny and it is true that it is warm outside).

Or

· The truth table for the or operator, ∨

· ∨is also called the disjunctive operator.

· A ∨B is the disjunction of A and B.

· Clearly A ∨B is true for any situation except when both A and B are false.

· If A is true, or if B is true, or if both A and B are true, A ∨B is true.

· This table represents the inclusive-or operator.

· A table to represent exclusive-or would have false in the final row. In other words, while A ∨B is true if A and B are both true, A EOR B

(A exclusive-or B) is false if A and B are both true.

· You may also notice a pleasing symmetry between the truth tables for ∧and ∨. This will become useful later, as will a number of other symmetrical

relationships.

Implies

· The truth table for implies (→) is a little less intuitive

· This form of implication is also known as material implication

· In the statement A→B, A is the antecedent, and B is the consequent. Thebottom two lines of the table should be obvious. If A is true and B is true, then A →􀀀B seems to be a reasonable thing to believe.

· For example, if A means “you live in France” and B means “You speak French,” then A→B corresponds to the statement “if you live in France, then you speak French.”

· Clearly, this statement is true (A→B is true) if I live in France and I speak French (A is true and B is true).

· Similarly, if I live in France, but I don’t speak French (A is true, but B is false), then it is clear that A→B is not true.

· The situations where A is false are a little less clear. If I do not live in France (A is not true), then the truth table tells us that regardless of whether I speak

· French or not (the value of B), the statement A→B is true. A→B is usually read as “A implies B” but can also be read as “If A then B” or “If A is true then B is true.”

· Hence, if A is false, the statement is not really saying anything about the value of B, so B is free to take on any value (as long as it is true or false, of course!).

· All of the following statements are valid:

             52 = 25 →4 = 4 (true →true)

             9 _ 9 = 123 →8 > 3 (false →true)

            52 = 25 →0 = 2 (false →false)

· In fact, in the second and third examples, the consequent could be given any meaning, and the statement would still be true. For example, the following

statement is valid: 52 = 25 →Logic is weird

· Notice that when looking at simple logical statements like these, there does not need to be any real-world relationship between the antecedent and the consequent.

· For logic to be useful, though, we tend to want the relationships being expressed to be meaningful as well as being logically true.

Iff

· The truth table for iff (if and only if {↔}) is as follows

· It can be seen that A ↔ B is true as long as A and B have the same value.

· In other words, if one is true and the other false, then A ↔ B is false. Otherwise, if A and B have the same value, A↔ B is true.

Complex Truth Tables

· Truth tables are not limited to showing the values for single operators.

· For example, a truth table can be used to display the possible values for A ∧(B ∨C).

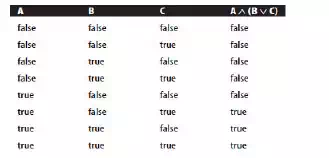
· Note that for two variables, the truth table has four lines, and for three variables, it has eight. In general, a truth table for n variables will have 2n lines.

· The use of brackets in this expression is important. A ∧(B ∨C) is not the same as (A∧B) ∨C.

· To avoid ambiguity, the logical operators are assigned precedence, as withmathematical operators.

· The order of precedence that is used is as follows: ￢, ∧, ∨,→,↔

· Hence, in a statement such as ￢A ∨ ￢B ∧ C, the ￢operator has the greatest precedence, meaning that it is most closely tied to its symbols. ∧ has a greater

precedence than ∨, which means that the sentence above can be expressed as (￢A) ∨ ((￢B) ∧C)

· Similarly, when we write ￢A ∨B this is the same as (￢A) ∨B rather than ￢(A ∨B)

· In general, it is a good idea to use brackets whenever an expression might otherwise be ambiguous.

Tautology

Consider the following truth table:

· This truth table has a property that we have not seen before: the value of the expression A∨￢A is true regardless of the value of A.

· An expression like this that is always true is called a tautology.

· If A is a tautology, we write: |=A

· A logical expression that is a tautology is often described as being valid.

· A valid expression is defined as being one that is true under any interpretation.

· In other words, no matter what meanings and values we assign to the variables in a valid expression, it will still be true.

· For example, the following sentences are all valid: If wibble is true, then wibble is true. Either wibble is true, or wibble is not true.

· In the language of logic, we can replace wibble with the symbol A, in which case these two statements can be rewritten as

            A→A

            A ∨￢A

· If an expression is false in any interpretation, it is described as being contradictory.

· The following expressions are contradictory:

           A ∧￢A

    ( A ∨￢A)→(A ∧ ￢A)

Equivalence

Consider the following two expressions:

A ∧ B

B ∧ A

· It should be fairly clear that these two expressions will always have the same value for a given pair of values for A and B.

· In otherwords, we say that the first expression is logically equivalent to the second expression.

· We write this as A ∧ B _ B ∧ A. This means that the ∧ operator is commutative.

· Note that this is not the same as implication: A ∧ B→B ∧ A, although this second statement is also true.

· The difference is that if for two expressions e1 and e2: e1 _ e2, then e1 will always have the same value as e2 for a given set of variables.

· On the other hand, as we have seen, e1→e2 is true if e1 is false and e2 is true.

· There are a number of logical equivalences that are extremely useful.

· The following is a list of a few of the most common:

A ∨ A _ A

A ∧ A _ A

A ∧ (B ∧ C) _ (A ∧ B) ∧C (∧ is associative)

A ∨ (B ∨ C) _ (A ∨ B) ∨C (∨ is associative)

A ∧ (B ∨ C) _ (A ∧ B) ∨ (A ∧ C) (∧ is distributive over ∨)

A ∧ (A ∨ B) _ A

A ∨ (A ∧ B) _ A

A ∧ true _ A

A ∧ false _ false

A ∨ true _ true

A ∨ false _ A

· All of these equivalences can be proved by drawing up the truth tables for each side of the equivalence and seeing if the two tables are the same.

· The following is a very important equivalence: A→B _ ￢A ∨ B

· We do not need to use the →􀀀 symbol at all—we can replace it with a combination of ￢and ∨.

· Similarly, the following equivalences mean we do not need to use ∧ or↔:

             A ∧ B _ ￢(￢A ∨ ￢B)

             A↔ B _ ￢(￢(￢A ∨ B) ∨ ￢ (￢B ∨ A))

· In fact, any binary logical operator can be expressed using ￢and ∨. This is a fact that is employed in electronic circuits, where nor gates, based on an operator called

           nor, are used. Nor is represented by ↓, and is defined as follows:

          A ↓ B _ ￢(A ∨ B)

· Finally, the following equivalences are known as DeMorgan’s Laws:

             A ∧ B _ ￢(￢A ∨ ￢B)

             A ∨ B _ ￢(￢A ∧ ￢B)

· By using these and other equivalences, logical expressions can be simplified.

· For example, (C ∧ D) ∨ ((C ∧ D) ∧ E) can be simplified using the following rule: A ∨ (A ∧ B) _ A hence, (C ∧ D) ∨ ((C ∧ D) ∧ E) _ C ∧ D

· In this way, it is possible to eliminate subexpressions that do not contribute to the overall value of the expression.