Constraint Satisfaction Search
· Search can be used to solve problems that are limited by constraints, such as the eightqueens problem. Such problems are often known as Constraint Satisfaction Problems, or CSPs. I
· n this problem, eight queens must be placed on a chess board in such a way that no two queens are on the same diagonal, row, or column. If we use traditional chess
board notation, we mark the columns with letters from a to g and the rows with numbers from 1 to 8. So, a square can be referred to by a letter and a number, such as
a4 or g7.
· This kind of problem is known as a constraint satisfaction problem (CSP) because a solution must be found that satisfies the constraints.
· In the case of the eight-queens problem, a search tree can be built that represents the possible positions of queens on the board. One way to represent this is to have a tree that is 8-ply deep, with a branching factor of 64 for the first level, 63 for the next level, and so on, down to 57 for the eighth level.
· A goal node in this tree is one that satisfies the constraints that no two queens can be on the same diagonal, row, or column.
· An extremely simplistic approach to solving this problem would be to analyze every possible configuration until one was found that matched the constraints.
· A more suitable approach to solving the eight-queens problem would be to use depthfirst search on a search tree that represents the problem in the following manner:
· The first branch from the root node would represent the first choice of a square for a queen. The next branch from these nodes would represent choices of where to place the second queen.
· The first level would have a branching factor of 64 because there are 64 possible squares on which to place the first queen. The next level would have a somewhat lower branching factor because once a queen has been placed, the constraints can be used to determine possible squares upon which the next queen can be placed.
· The branching factor will decrease as the algorithm searches down the tree. At some point, the tree will terminate because the path being followed will lead to
a position where no more queens can be placed on legal squares on the board, and there are still some queens remaining.

In fact, because each row and each column must contain exactly one queen, the branching factor can be significantly reduced by assuming that the first queen must be placed in row 1, the second in row 2, and so on. In this way, the first level will have a branching factor of 8 (a choice of eight squares on which the first queen can be placed), the next 7, the next 6, and so on.
The search tree can be further simplified as each queen placed on the board “uses up”
a diagonal, meaning that the branching factor is only 5 or 6 after the first choice has
been made, depending on whether the first queen is placed on an edge of the board
(columns a or h) or not.
· The next level will have a branching factor of about 4, and the next may have a branching factor of just 2, as shown in Fig 6.1.
· The arrows in Fig 6.1 show the squares to which each queen can move.
· Note that no queen can move to a square that is already occupied by another queen.

· In Fig 6.1, the first queen was placed in column a of row 8, leaving six choices for the next row. The second queen was placed in column d of row 7, leaving four choices for row 6. The third queen was placed in column f in row 6, leaving just two choices (column c or column h) for row 5.
· Using knowledge like this about the problem that is being solved can help to significantly reduce the size of the search tree and thus improve the efficiency of the
search solution.
· A solution will be found when the algorithm reaches depth 8 and successfully places the final queen on a legal square on the board.
· A goal node would be a path containing eight squares such that no two squares shared a diagonal, row, or column.
· One solution to the eight-queens problem is shown in above Fig .
· Note that in this solution, if we start by placing queens on squares e8, c7, h6, and then d5, once the fourth queen has been placed, there are only two choices for placing the fifth queen (b4 or g4). If b4 is chosen, then this leaves no squares that could be chosen for the final three queens to satisfy the constraints. If g4 is chosen for the fifth queen, as has been done in Fig 6.2, only one square is available for the sixth queen (a3), and the final two choices are similarly constrained. So, it can be seen that by applying the constraints appropriately, the search tree can be significantly reduced for this problem.
· Using chronological backtracking in solving the eight-queens problem might not be the most efficient way to identify a solution because it will backtrack over moves that did not necessarily directly lead to an error, as well as ones that did. In this case, nonchronological backtracking, or dependency-directed backtracking could be more useful because it could identify the steps earlier in the search tree that caused the problem further down the tree.
Forward Checking
· In fact, backtracking can be augmented in solving problems like the eightqueens problem by using a method called forward checking.
· As each queen is placed on the board, a forward-checking mechanism is used to delete from the set of possible future choices any that have been rendered impossible by placing the queen on that square.
· For example, if a queen is placed on square a1, forward checking will remove all squares in row 1, all squares in column a, and also squares b2, c3, d4, e5, f6, g7, and h8.
· In this way, if placing a queen on the board results in removing all remaining squares, the system can immediately backtrack, without having to attempt to place any more queens.
· This can often significantly improve the performance of solutions for CSPs such as the eight-queens problem.
Most-Constrained Variables
· A further improvement in performance can be achieved by using the most-constrained variable heuristic.
· At each stage of the search, this heuristic involves working with the variable that has the least possible number of valid choices.
· In the case of the eight-queens problem, this might be achieved by considering the problem to be one of assigning a value to eight variables, a through h. Assigning value 1 to variable a means placing a queen in square a1.
· To use the most constrained variable heuristic with this representation means that at each move we assign a value to the variable that has the least choices available to it. Hence, after assigning a = 1, b = 3, and c = 5, this leaves three choices for d, three choices for e, one choice for f, three choices for g, and three choices for h. Hence, our next move is to place a queen in column f.
· This heuristic is perhaps more clearly understood in relation to the mapcoloring problem. It makes sense that, in a situation where a particular country can be given
only one color due to the colors that have been assigned to its neighbors, that country be colored next.
· The most-constraining variable heuristic is similar in that it involves assigning a value next to the variable that places the greatest number of constraints on future variables.
· The least-constraining value heuristic is perhaps more intuitive than the two already presented in this section.
· This heuristic involves assigning a value to a variable that leaves the greatest number of choices for other variables.
· This heuristic can be used to make n-queens problems with extremely large values of n quite solvable.
Example: Cryptographic Problems
Ř The constraint satisfaction procedure is also a useful way to solve problems such as cryptographic problems. For example:
FORTY
+ TEN
+ TEN
SIXTY
Solution:
29786
+ 850
+ 850
31486
· This cryptographic problem can be solved by using a Generate and Test method, applying the following constraints:
· Each letter represents exactly one number.
· No two letters represent the same number.
· Generate and Test is a brute-force method, which in this case involves cycling through all possible assignments of numbers to letters until a set is found that meets
the constraints and solves the problem.
· Without using constraints, the method would first start by attempting to assign 0 to all letters, resulting in the following sum:
00000
+ 000
+ 000
00000
· Although this may appear to be a valid solution to the problem, it does not meet the constraints laid down that specify that each letter can be assigned only one number, and each number can be assigned only to one letter.
· Hence, constraints are necessary simply to find the correct solution to the problem. They also enable us to reduce the size of the search tree.
· In this case, for example, it is not necessary to examine possible solutions where two letters have been assigned the same number, which dramatically reduces the possible solutions to be examined.
Heuristic Repair
· Heuristics can be used to improve performance of solutions to constraint satisfaction problems.
· One way to do this is to use a heuristic repair method, which involves generating a possible solution (randomly, or using a heuristic to generate a position that is close to a solution) and then making changes that reduce the distance of the state from the goal.
· In the case of the eight-queens problem, this could be done using the minconflicts heuristic.
· To move from one state to another state that is likely to be closer to a solution using the min-conflicts heuristic, select one queen that conflicts with another queen (in other words, it is on the same row, column, or diagonal as another queen).
· Now move that queen to a square where it conflicts with as few queens as possible. Continue with another queen. To see how this method would work, consider the
starting position shown in Fig 6.3.
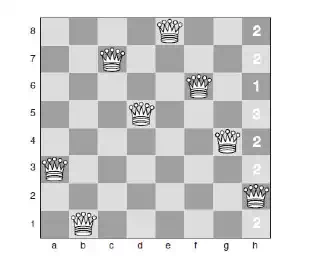
· This starting position has been generated by placing the queens such that there are no conflicts on rows or columns. The only conflict here is that the queen in column 3 (on c7) is on a diagonal with the queen in column h (on h2).
To move toward a solution, we choose to move the queen that is on column h.
· We will only ever apply a move that keeps a queen on the same column because we already know that we need to have one queen on each column.
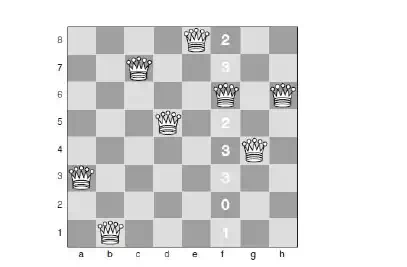
· Each square in column h has been marked with a number to show how many other queens that square conflicts with. Our first move will be to move the queen on column h up to row 6, where it will conflict only with one queen. Then we arrive at the position shown in below Fig
· Because we have created a new conflict with the queen on row 6 (on f6), our next move must be to move this queen. In fact, we can move it to a square where it has
zero conflicts. This means the problem has been solved, and there are no remaining conflicts.
· This method can be used not only to solve the eight-queens problem but also has been successfully applied to the n-queens problem for extremely large values of n. It has been shown that, using this method, the 1,000,000 queens problem can be solved in an average of around 50 steps.
· Solving the 1,000,000-queens problem using traditional search techniques would be impossible because it would involve searching a tree with a branching factor of 1012.
Local Search and Metaheuristics
· Local search methods work by starting from some initial configuration (usually random) and making small changes to the configuration until a state is reached from
which no better state can be achieved.
· Hill climbing is a good example of a local search technique.
· Local search techniques, used in this way, suffer from the same problems as hill climbing and, in particular, are prone to finding local maxima that are not the best
solution possible.
· The methods used by local search techniques are known as metaheuristics.
· Examples of metaheuristics include simulated annealing, tabu search, genetic algorithms, ant colony optimization, and neural networks.
· This kind of search method is also known as local optimization because it is attempting to optimize a set of values but will often find local maxima rather than a
global maximum.
· A local search technique applied to the problem of allocating teachers to classrooms would start from a random position and make small changes until a configuration was reached where no inappropriate allocations were made.
Exchanging Heuristics
· The simplest form of local search is to use an exchanging heuristic.
· An exchanging heuristic moves from one state to another by exchanging one or more variables by giving them different values. We saw this in solving the
eight-queens problem as heuristic repair.
· A k-exchange is considered to be a method where k variables have their values changed at each step.
· The heuristic repair method we applied to the eight-queens problem was 2-exchange.
· A k-exchange can be used to solve the traveling salesman problem. A tour (a route through the cities that visits each city once, and returns to the start) is generated at random. Then, if we use 2-exchange, we remove two edges from the tour and substitute them for two other edges. If this pro duces a valid tour that is shorter than the previous one, we move on from here. Otherwise, we go back to the previous tour and try a different set of substitutions.
· In fact, using k = 2 does not work well for the traveling salesman problem, whereas using k = 3 produces good results.
· Using larger numbers of k will give better and better results but will also require more and more iterations.
· Using k = 3 gives reasonable results and can be implemented efficiently. It does, of course, risk finding local maxima, as is often the case with local
search methods.
Iterated Local Search
· Iterated local search techniques attempt to overcome the problem of local maxima by running the optimization procedure repeatedly, from different
initial states.
· If used with sufficient iterations, this kind of method will almost always find a global maximum.
· The aim, of course, in running methods like this is to provide a very good solution without needing to exhaustively search the entire problem space.
· In problems such as the traveling salesman problem, where the search space grows extremely quickly as the number of cities increases, results can be generated that are good enough (i.e., a local maximum) without using many iterations, where a perfect solution would be impossible to find (or at least it would be impossible to guarantee a perfect solution even one iteration of local search may happen upon the global maximum).
Tabu Search
· Tabu search is a metaheuristic that uses a list of states that have already been visited to attempt to avoid repeating paths.
· The tabu search metaheuristic is used in combination with another heuristic and operates on the principle that it is worth going down a path that appears to be poor if it avoids following a path that has already been visited.
· In this way, tabu search is able to avoid local maxima.