Beta Distribution

The beta distribution represents continuous probability distribution parametrized by two positive shape parameters, αα and ββ, which appear as exponents of the random variable x and control the shape of the distribution.

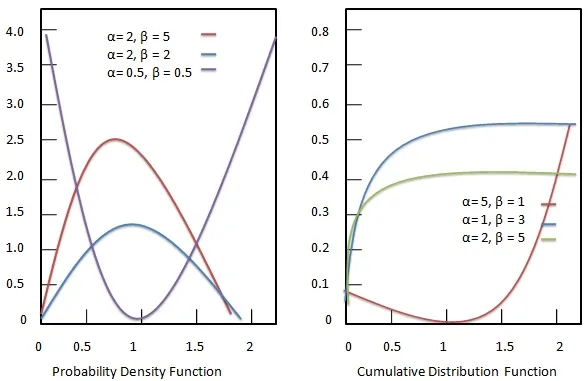
Probability density function

Probability density function of Beta distribution is given as:

Formula

f(x)=(x−a)α−1(b−x)β−1B(α,β)(b−a)α+β−1a≤x≤b;α,β>0where B(α,β)=∫10tα−1(1−t)β−1dtf(x)=(x−a)α−1(b−x)β−1B(α,β)(b−a)α+β−1a≤x≤b;α,β>0where B(α,β)=∫01tα−1(1−t)β−1dt

Where −

· α,βα,β = shape parameters.

· a,ba,b = upper and lower bounds.

· B(α,β)B(α,β) = Beta function.

Standard Beta Distribution

In case of having upper and lower bounds as 1 and 0, beta distribution is called the standard beta distribution. It is driven by following formula:

Formula

f(x)=xα−1(1−x)β−1B(α,β)≤x≤1;α,β>0f(x)=xα−1(1−x)β−1B(α,β)≤x≤1;α,β>0

Cumulative distribution function

Cumulative distribution function of Beta distribution is given as:

Formula

F(x)=Ix(α,β)=∫x0tα−1(1−t)β−1dtB(α,β)0≤x≤1;p,β>0F(x)=Ix(α,β)=∫0xtα−1(1−t)β−1dtB(α,β)0≤x≤1;p,β>0

Where −

· α,βα,β = shape parameters.

· a,ba,b = upper and lower bounds.

· B(α,β)B(α,β) = Beta function.

It is also called incomplete beta function ratio.

Binomial Distribution

Bionominal appropriation is a discrete likelihood conveyance. This distribution was discovered by a Swiss Mathematician James Bernoulli. It is used in such situation where an experiment results in two possibilities - success and failure. Binomial distribution is a discrete probability distribution which expresses the probability of one set of two alternatives-successes (p) and failure (q). Binomial distribution is defined and given by the following probability function:

Formula

P(X−x)=nCxQn−x.pxP(X−x)=nCxQn−x.px

Where −

· pp = Probability of success.

· qq = Probability of failure = 1−p1−p.

· nn = Number of trials.

· P(X−x)P(X−x) = Probability of x successes in n trials.

Example

Problem Statement:

Eight coins are tossed at the same time. Discover the likelihood of getting no less than 6 heads.

Solution:

Let pp=probability of getting a head. qq=probability of getting a tail.

Here,p=12,q=12,n=8, P(X−x)=nCxQn−x.px,P(at least 6 heads)=P(6H)+P(7H)+P(8H),8C6(12)2(12)6+8C7(12)1(12)7+8C8(12)8,=28×1256+8×1256+1×1256,=37256