Gamma Distribution

The gamma distribution represents continuous probability distributions of two-parameter family. Gamma distributions are devised with generally three kind of parameter combinations.

· A shape parameter kk and a scale parameter θθ.

· A shape parameter α=kα=k and an inverse scale parameter β=1θβ=1θ, called as rate parameter.

· A shape parameter kk and a mean parameter μ=kβμ=kβ.

Each parameter is a positive real numbers. The gamma distribution is the maximum entropy probability distribution driven by following criteria.

Formula

E[X]=kθ=αβ>0 and is fixed.E[ln(X)]=ψ(k)+ln(θ)=ψ(α)−ln(β) and is fixed.E[X]=kθ=αβ>0 and is fixed.E[ln(X)]=ψ(k)+ln(θ)=ψ(α)−ln(β) and is fixed.

Where −

· XX = Random variable.

· ψψ = digamma function.

Characterization using shape αα and rate ββ

Probability density function

Probability density function of Gamma distribution is given as:

Formula

f(x;α,β)=βαxα−1e−xβΓ(α) where x≥0 and α,β>0f(x;α,β)=βαxα−1e−xβΓ(α) where x≥0 and α,β>0

Where −

· αα = location parameter.

· ββ = scale parameter.

· xx = random variable.

Cumulative distribution function

Cumulative distribution function of Gamma distribution is given as:

Formula

F(x;α,β)=∫x0f(u;α,β)du=γ(α,βx)Γ(α)F(x;α,β)=∫0xf(u;α,β)du=γ(α,βx)Γ(α)

Where −

· αα = location parameter.

· ββ = scale parameter.

· xx = random variable.

· γ(α,βx)γ(α,βx) = lower incomplete gamma function.

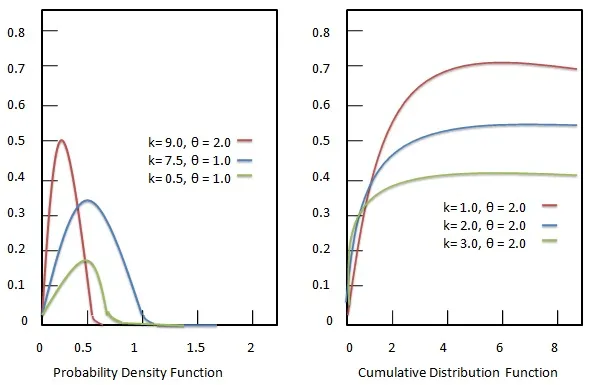
Characterization using shape kk and scale θθ

Probability density function

Probability density function of Gamma distribution is given as:

Formula

f(x;k,θ)=xk−1e−xθθkΓ(k) where x>0 and k,θ>0f(x;k,θ)=xk−1e−xθθkΓ(k) where x>0 and k,θ>0

Where −

· kk = shape parameter.

· θθ = scale parameter.

· xx = random variable.

· Γ(k)Γ(k) = gamma function evaluated at k.

Cumulative distribution function

Cumulative distribution function of Gamma distribution is given as:

Formula

F(x;k,θ)=∫x0f(u;k,θ)du=γ(k,xθ)Γ(k)F(x;k,θ)=∫0xf(u;k,θ)du=γ(k,xθ)Γ(k)

Where −

· kk = shape parameter.

· θθ = scale parameter.

· xx = random variable.

· γ(k,xθ)γ(k,xθ) = lower incomplete gamma function.